Comp 353/453: Database Programming, Corboy 523, 7:00 Thursdays

Week 5, Feb 16

Read in Elmasri & Navathe (EN)

Here is an external site with some useful SQL examples: sqlzoo.net.


See here for an example from last week of the power of not exists.

I've rewritten last week's notes on "ALL" queries. See them here.

Another ALL example:

    List departments that are at all locations

This doesn't mean every location in the world; it means all the locations in the list
    select distinct dlocation from dept_locations;

First of all, if we try
    select distinct dlocation from dept_locations;
we get the list Houston, Stafford, Bellaire, Sugarland. But if we query
    select * from dept_locations
we get
+---------+-----------+
|       1 | Houston   |
|       4 | Stafford  |
|       5 | Bellaire  |
|       5 | Houston   |
|       5 | Sugarland |
+---------+-----------+
So to have a nonempty result, we have to insert a record:
    insert into dept_locations values(5, 'Stafford');
    delete from dept_locations where dnumber = 5 and dlocation = 'Stafford';

If we want two entries, we can
    insert into dept_locations values (1, 'Stafford'), (1, 'Bellaire'), (1, 'Sugarland');
    delete from dept_locations where dnumber = 1 and dlocation in ('Stafford', 'Bellaire', 'Sugarland');

As we did last week, we will approach "departments d at all locations" by first changing to the equivalent "departments d for which there does not exist a location that d is not located at", or "departments d for which there does not exist a location L such that d is not located at L".

The next step is to transform "d is located at L" to SQL:
    exists (select * from dept_locations loc2 where loc2.dnumber = d.dno and loc2.dlocation = L)
(locations L are simple strings, not some larger record as department d was). To change this to "d is not located at L", we just change exists to not exists. I used the name "loc2" because the outer query will use name loc1.

We now say "there does not exist a location L such that d is not located at L" as

not exists (select * from dept_locations loc1 where not exists
    (select * from dept_locations loc2 where loc2.dnumber = d.dnumber and loc2.dlocation = loc1.dlocation))

To finish it off, we put "select d.dno from department d where" in front of it:

select d.dnumber from department d where not exists (select * from dept_locations loc1 where not exists
    (select * from dept_locations loc2 where loc2.dnumber = d.dnumber and loc2.dlocation = loc1.dlocation))

This looks circular, or like the loc2 name is redundant, but it's not: the loc2 record refers to a possible location of department d; loc1 refers to any other location.
Another way to look at this is that for every loc1 (every possible location) there is a loc2 at the same location that matches d.


Triggers

Chapter 4 had two uses of the CHECK statement (neither of which we did at the time): attribute checks and record checks. Two further checks are assertions and triggers. These sometimes have efficiency consequences, however.

1. Attribute checks

example: for the department table,
    dnumber INT not null check (dnumber >0 and dnumber < 100)
These are applied whenever an individual attribute is set.

Here's another important attribute check (MySQL syntax)

create table employee2 (
    name varchar(50) not null,
    ssn    char(9) primary key not null,
    dno   INT not null check (dno > 0 and dno < 100),
    check (ssn RLIKE  '[0-9][0-9][0-9][0-9][0-9][0-9][0-9][0-9][0-9]')
) engine innodb;

We can populate this from table employee:

insert into employee2
select e.lname, e.ssn, e.dno from employee e;

Some additional insertions that should fail:

insert into employee2 values ('anonymous', 'anonymous', 37);
insert into employee2 values ('joe hacker', '12345678O', 37);       // that is the letter 'O'
insert into employee2 values ('jack hack',  '12345689', 25);          // not enough digits

They do not fail! MySQL ignores checks (even on dno). Actually, MySQL does not even check that there are parentheses around the body of the check condition.

How about postgres?

create table employee2 (
    name varchar(50) not null,
    ssn    char(9) primary key not null,
    dno   INT not null check (dno > 0 and dno < 100),
    check (ssn SIMILAR TO  '[0-9][0-9][0-9][0-9][0-9][0-9][0-9][0-9][0-9]')
);

This should work.

You can also do this in postgres:

create table employee3 (
    name varchar(50) not null,
    ssn    char(9) primary key not null,
    dno   INT not null check (dno > 0 and dno < 100),
    check (char_length(ssn) = 9)
);

2. Record (tuple) checks

create table DEPARTMENT (
       dname ....
       dnumber ...
       mgr_ssn ...
       mgr_start   DATE   not null,
       dept_creation  DATE   not null,
       check (dept_creation <= mgr_start)
);

These are applied whenever a particular row is updated or added to that table.


3. Assertions

Assertions are general requirements on the entire database, to be maintained at all times.

create assertion salary_constraint
check ( not exists
(select * from employee e, employee s, department d
where e.salary > s.salary and e.dno = d.dnumber and d.mgr_ssn = s.ssn)
);

The problem with this (aside from the fact that this is not always a good business idea) is when and where it is applied. After every database update? But only some updates even potentially result in violations: changes to employee salaries, and changes of manager.

From the manual:
    PostgreSQL does not implement assertions at present.

4. Triggers

Due to the "expense" of assertions, some databases (eg Oracle) support triggers: assertions that are only checked at user-specified times (eg update or insert into a particular table).

create trigger salary_violation
before insert or update of salary, super_ssn on employee
for each row when (new.salary >
(select salary from employee e
where e.ssn = new.super_ssn))
inform_supervisor (New.supervisor_ssn, new.ssn)         -- some prepared external procedure
);

In postgres, we'd finish off with
    for each row execute procedure inform_supervisor);
That is, we can't have the when clause.

Writing the external procedures is beyond the scope of SQL.

VIEWS

Here's a simple view, that is, a sort of "virtual table". The view is determined by the select statement within. The point, though, is not that we set works_on1 here to be the output of the select, but that as future changes are made to the underlying tables, the view is automatically updated.

create view works_on1 AS
select e.fname, e.lname, p.pname, w.hours
from employee e, project p, works_on w
where e.ssn = w.essn and w.pno= p.pnumber;

We can now do:

select * from works_on1;

select w.lname, sum(w.hours)
from works_on1 w
group by w.lname;

Now let's add an employee:

insert into employee values ('Ralph', null, 'Wiggums', '000000001', '1967-03-15', null, 'M', 22000, '333445555', 5);
insert into works_on values ('000000001', 1, 9.8);

Ralph is there (working on 'ProductX'). To delete:

delete from works_on where essn='000000001';
delete from employee where ssn='000000001';

Here's a typical use of views for a single table: hiding some columns (I've hidden salary for privacy reasons, and address for space):

create view employee1 AS
select fname, minit, lname, ssn, bdate, sex, super_ssn, dno from employee;

Finally, here's another example from the book, demonstrating column renaming and use of aggregation columns:

create view deptinfo (dept_name, employee_count, total_salary) AS
select d.dname, count(*), sum(e.salary)
from department d, EMPLOYEE e
where d.dnumber = e.dno
group by dname;

There are two primary implementation strategies for views:
It is typically a problem to update views, though we can do this for the employee1 view so long as the missing fields do not have not null constraints (and also that we include the underlying employee table's primary key in the view).

In creating mailing lists for Microsoft Access, a given list is based not on a query (which would make the most sense), but on a named view.

Schema change

We've already seen ALTER TABLE in use: we used it to add foreign key constraints after some initial values were entered:

alter table employee add foreign key (dno) references department(dnumber);

Another application is for schema changes as the database needs evolve.

Oracle ROWNUM

Oracle allows the use of the "virtual" column rownum when working with sorted tables. This way one can print the third-highest value, for example (where rownum = 3), or the top 10 values (where rownum <=10).



Relational Algebra


We'll only do a quick look at this. The point is that SQL has a precise mathematical foundation; this allows the query optimizer to rewrite queries (ie to "prove" that alternative forms of some queries are equivalent).

First some set-theoretic notations:

Union:  R1 ∪ R2, where R1, R2 are subsets of same cross product (that is, they are sets of tuples of the same type). This is logically like OR

Intersection: Logically like AND

Difference: Logical "R1 but NOT R2"

    R1 − R2

The basic relational operations are:
   
PROJECTION: selecting some designated columns, ie taking some vertical slices from a relation. Projection corresponds to the select col1, col2, etc part of the query. It is denoted with π, subscripted with column names: πlname,salary(R).
   
SELECTION: Here we specify a Boolean condition that selects only some rows of a relation; this corresponds to the where part of a SQL query
This is denoted by σ, subscripted with the condition: σdno=5 AND salary>=30000(R)

More examlples can be found on pp 147-149 of E&N.


PRODUCT: The product R×S is the set of ordered pairs {⟨r,s⟩ | r∈R and s∈S}. The product can be of two  tables (relations) as well as of two domains; in this case, if r=⟨r1,r2,...,rn⟩ and s=⟨s1,s2,...,sk⟩, then we likely identify the pair ⟨r,s⟩ with the n+k-tuple ⟨r1,r2,...,rn,s1,s2,...,sk⟩.


   
JOIN

The join represents all records from table R and table S where R.colN = S.colM
The traditional notation for this is R⋈S, or, when we wish to make the join condition explicit, R⋈colN=colMS. If the join column has the same name in both R and S, we may just subscript with that column name: R⋈ssnS.

The join can be expressed as Product,Selection,Projection as follows:

   πwhatever cols we need to keep (σcolN=colM(R×S))
   
In other words, the join is not a "fundamental" operation; contrast this with the "outer join" below. As a suggestion for implementation, the above is not very efficient: we never want to form the entire product R×S. But this notation lets us restructure the query for later optimization.

The equijoin is a join where the join condition involves the equality operation; this is the most common.
The natural join is a join where we delete one of the two identical columns of an equijoin. That is, if R is ⟨ssn,lname⟩ and S is ⟨ssn, proj⟩, then the equijoin is really ⟨ssn,lname,ssn,proj⟩, where the two ssns are equal, and the natural join is ⟨ssn,lname,proj⟩.

Note that the outer join can not be expressed this way; the outer join of two relations R and S is not necessarily a subset of R×S (though it may be subset of R×(S ∪ {NULL}). The outer join is fundamentally about allowing NULL values. If foo is the name of the join column in R, the outer join is of the form

    R⋈S  ∪  (σfoo∉π_foo(S) (R) × {NULL})

(Explain)
Note the condition here is strictly speaking outside the scope of the Boolean expressions at the bottom of page 147 of E&N.


Division:  R ÷ S: As above, we identify R with a relation T×S; R÷S is then {t∈T| ∀s∈S ⟨t,s⟩∈R} ("∀s∈S" means "for all s in S"). In English, which records in T appear combined with EVERY row of S.

As an example, let E be the employees table, and P be the projects, and W be the Works_on table, a subset of E×P. Then W ÷ P is the set of employees who have worked on every project; W ÷ E is the set of projects worked on by every employee. Note the implicit "closed world" hypothesis: we're only considering project numbers (or employee numbers) that actually appear in P and E.

Note the prerequisite that R is a table "extending" that of S: R has all the columns that S has, and more. The underlying set of columns of R ÷ S is the set (columns of R) − (columns of S). It is usually easier to think of division as being of the form T×S ÷ S.

Asking which students got only A's is not quite an example of this (why?)

The book also defines a rename operation; for certain purposes this is important but I classify it as "syntactic sugar".

The book also uses an assignment operator (TEMP ← σcolN=colM(R×S)). However, we can always substitute the original expression in for the TEMP variable.

Query trees

Here is figure 6.9 from EN6 page 165. The question is for every project located in Stafford, list the project number, the controlling deparment number, and the department manager's last name, address and birth date. In SQL this is.

select   p.pnumber, p.dnum, e.lname, e.address, e.bdate
from    project p, department d, employee e
where  p.dnum = d.dnumber and d.mgr_ssn = e.ssn and p.plocation = 'Stafford'

Here is this query in a query-tree representation:

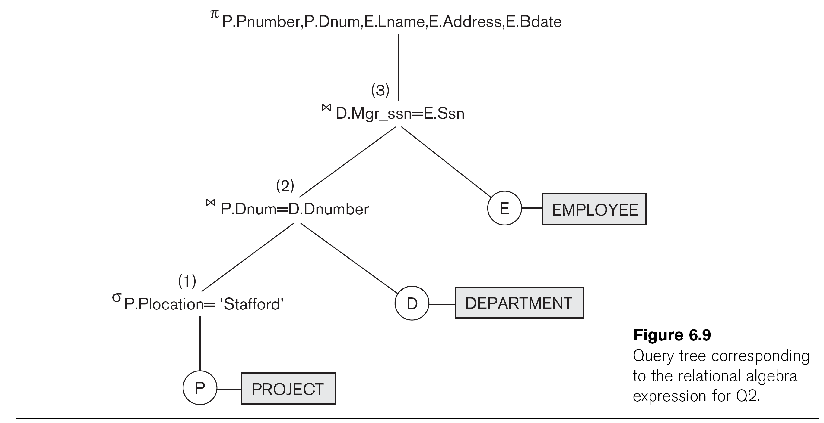
query tree


Note that the tree allows us to express the solution as a SEQUENCE of steps.

Another double-join example, listing employees and the projects they worked on.

Select e.lname, p.pname from employee e, works_on w, project p
where e.ssn = w.essn and w.pno = p.pnumber;



Entity-Relationship modeling

This is a variant (actually a predecessor) of object modeling (eg UML or CRC cards or Booch diagrams). In the latter, everything is an object. In ER modeling, we will make a distinction between entities (things) and relationships. As a simple example, students and courses are entities; but the enrolled_in table is a relationship. Sections most likely would be modeled as entities too, though there is a relationship to COURSE.

The ER process starts, like most software-engineering projects, with obtaining requirements from users. What data needs to be kept, what queries need to be asked, and what business rules do we build in? (For example, if the DEPARTMENT table has a single column for manager, then we have just committed to having a single manager for each department.)

The goal of the E-R modeling process is to create an E-R diagram, which we can then more-or-less mechanically convert to a set of tables. Both entities and relationships will correspond to tables; entity tables will often have a single-attribute primary key while the key for relationship tables will almost always involve multiple attributes.

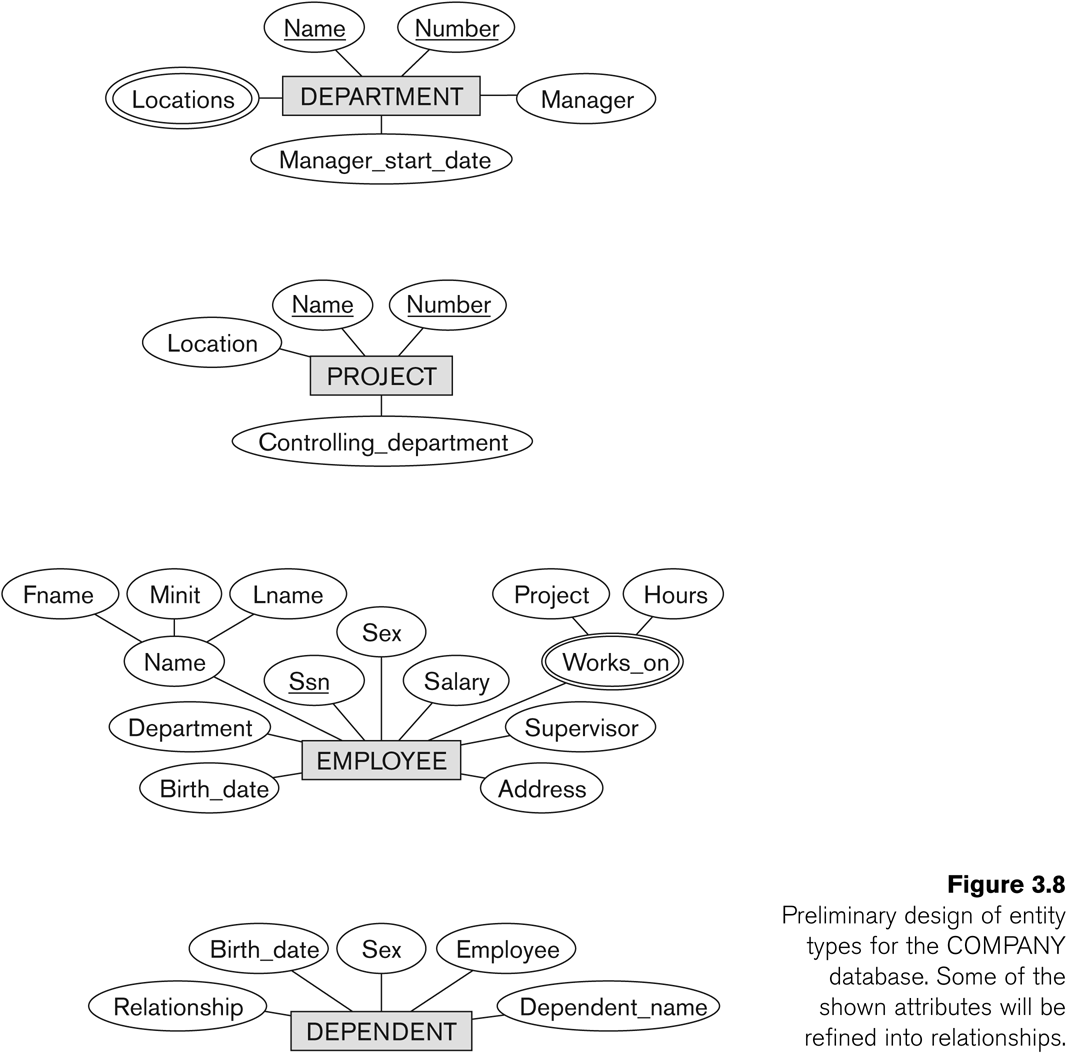
Here is an E-R diagram for the OFFICE database.  (The figure below was Fig 3.2 in an earlier edition of E&N; it is Fig 7.2 in the 6th edition.)

E-R diagram for COMPANY database

Entities

After the above beginnings, we identify the entities. These should represent physical things, such as employees or parts or (more abstractly) departments. Note that customer_orders might be modeled as an entity, but might also be modeled as a relationship.

Entities have attributes, which will later more or less become the fields. For each attribute we have the following aspects:
We also must decide which attributes can be NULL.

Attributes at this point should not be references to other tables; instead, we will create those references when we create relationships.

The book uses () to represent sub-attributes of composite attributes, and {} to surround multi-valued attributes.

Traditionally we represent the entity with a rectangular box, and the attributes are little oval tags.

An entity type is our resulting schema for the entity; the entity set is the actual set of entities.

In the diagram, we will underline the key attributes. If a key is composite, say (state,regnum), then we make a composite attribute out of those pieces.

This is a slight problem if the key can be either (state,regnum) or (state,license_plate); how could we best address this?

Note that key attributes really represent constraints.

In the early stages, we allowed entity attributes to be composite or computed or multi-valued; all of these will eventually be handled in specific ways as we translate into SQL.

Often there is more than one way to do things. In the COMPANY example, we might list dept as an attribute of EMPLOYEE, and eventually conclude that because dept represented an instance of another entity (DEPARTMENT), we would have a foreign-key constraint on EMPLOYEE.dept, referring to DEPARTMENT.dnumber.

Note, however, that we could instead list employees as a multi-valued attribute of DEPARTMENT. One reason for not doing this is that we do want to minimize the use of multi-valued attributes, but this arrangement would have been a possible option. Later, we even could implement this second approach by adding an attribute dept to the EMPLOYEE table (the table, not entity).

We actually could have both forms, but we would need to understand the constraint that if employee e is in the employees multi-valued attribute for DEPARTMENT d, then department d must be be the value of the EMPLOYEE e's dept attribute. That is, the dual attributes would have to be inverses.

As for naming entities, a common practice (used by E&N) is to name them with singular nouns. Nouns because they should represent things; singular for the individual objects. Eventually we will have a table of employees, plural, but we call it EMPLOYEE to represent what entities it contains.

Weak entities

The usual definition of a weak entity is that it is an entity that does not have key attributes of its own. The classic example is the DEPENDENT entity, with attributes name, birth_date, sex and relationship; a dependent is uniquely determined by the name and the employee to whom the dependent is associated. You might wonder why we don't add an attribute employee at the beginning, and have ⟨name, employee⟩ be the key. One problem with that approach is that employee is a reference to a different entity; such references should really be described as relationships. After all, the EMPLOYEE is really someone else, not an attribute of the DEPENDENT person itself (at least not in the same sense as bdate, age, etc). We will say, instead, that there is a relationship between the DEPENDENT entity and EMPLOYEE; this relationship is the identifying relationship for DEPENDENT.

In general, during the design process, the statement that "dependents do not have a key" is subject to interpretation; we can always declare that the associated employee's SSN is part of the key. However, the point is that dependents do not have a "natural" key that is an attribute of the dependent itself. Also, using the "employee_ssn" as an attribute is suspect because it realistically is an attempt to refer to another table.

There is a total participation constraint between DEPENDENT and EMPLOYEE; every DEPENDENT must be connected to some EMPLOYEE. As the book points out, however, every DRIVERS_LICENSE is associated with some PERSON, but the DRIVERS_LICENSE entity does in fact have its own key: the drivers_license_number.

The way that DEPENDENT could become a strong entity is if we added its own key: dependent_ssn. But typically the SSNs of dependents are not known (minor dependents may not even have SSNs), so we choose not to implement the database this way.

The DEPENDENT entity does have a partial key: the attribute name, which, together with the associated EMPLOYEE object, does define a key.

We could also represent dependents as a multi-valued, composite attribute of EMPLOYEE.

Fig 7.8 (6th-edition numbering) lists all the entities:

basic entities