Modulation and Transmission

Peter Dordal, Loyola University CS Department


How do we transmit sound (or any other analog or digital signal) using electromagnetic waves? We modulate the EM wave (the carrier) in order to encode the signal. The result no longer is a single frequency; it is a band of frequencies. This spreading of the single-frequency carrier to a band of frequencies is fundamental.

If we are sending the signal a long way (over transmission lines), then we may very well also need to modulate some form of carrier. In the digital context, this is sometimes known as encoding.

Example

Suppose we want to transmit a square wave, alternating from -1 to +1. We have a band-width of 4 Mhz. How does the data rate ("bandwidth" in the digital sense) compare to the band-width in the spectrum sense? The simple modulation here is an attempt to generate a square wave out of sine waves.

Case 1: we use sin(2πœ‹ft) + (1/3)sin(2πœ‹(3f)t) + (1/5)sin(2πœ‹(5f)t) (that is, three terms of the Fourier series), where f = 1 Mhz.
Look at this with fourier.xls: does it look squarish?
The frequencies are 1 Mhz, 3 Mhz and 5 Mhz. The band-width is 5-1 = 4 Mhz.
The data rate is 2 Mbps (sort of; we are sending 1 M 1-bits and 1 M 0-bits per second)

Note dependence on notion of what waveform is "good enough"

Case 2: If we double all the frequencies to 2 MHz, 6 MHz, 10 MHz, we get band-width 8MHz, data rate 4Mbps. This is the same as above with f=2 Mhz.

Case 3: We decide in the second case that we do not need the 10 MHz component, due to a more accurate receiver. The base frequency is f = 2MHz, frequencies 2MHz, 6MHz, band-width is now 6MHz - 2MHz = 4MHz, data rate: 4Mbps

Look at this with fourier.xls.

Note that we're really not carrying data in a meaningful sense; we can't send an arbitrary sequence of 0's and 1's this way. However, that's done mostly to simplify things.

Note also the implicit dependence on bandwidth of the fact that we're decomposing into sinusoidal waves.

Voice transmission: frequency band-width ~ 3-4kHz  (eg 300 Hz to 3300 Hz)
64Kbps encoding (8 bits sampled 8000 times a second)

Modems have the reverse job: given the band-width of ~3 kHz, they have to send at 56 kbps!

Note: we're looking at DISCRETE frequency spectrum (periodic signals). CONTINUOUS frequency spectrum also makes mathematical sense, but is kind of technical

Note that frequency-domain notion depends on fundamental theorem of Fourier analysis that every periodic function can be expressed as sum of sines & cosines (all with period an integral multiple of original)


Band-width of voice: <=4 kHz

This is quite a different meaning of band-width from the digital usage, where a 64kbps channel needs a bandwidth of 64kbps.

But if we wanted to encode the digitized voice back into an analog voice band-width, we'd have to encode 16 bits per cycle (Hertz), which is a little tricky.


Amplitude modulation & band-width
Note that AM modulation (ALL modulation, in fact) requires a "band-width"; ie range of frequencies. This will be very important for cellular.

AM:amplitude = [1+data(t)]*sin(2πœ‹ft)
f is "carrier" high frequency; eg 100,000


If data(t) = sin(2πœ‹gt), g a much lower frequency (eg 1000)
Then sin(2πœ‹ft)*sin(2πœ‹gt) = 0.5 cos(2πœ‹(f-g)t) - 0.5 cos(2πœ‹(f+g)t)

band of frequencies: (f-g) to (f+g)
band-width: 2g

Example: beats+modulation.xls, beats+modulation.ods


The sincfilter.ods spreadsheet, demonstrating filtering.

Note that most of the low-pass filtering is done within the first full cycle.

Discussion of the graph

Transmission

analog transmission: needs amplifiers to overcome attenuation
digital transmission: store-and-forward switches?
Switches do signal regeneration, not amplification; noise is NOT added. BUT: we need them a lot more often.


data may need some form of encoding: analog may use something like AM modulation, or equalization.

Digital encoding: NRZ is basic (1=on, 0=off), but isn't good in real life.

Analog data:

        Analog signal: commonly some form of modulation on a different frequency

        Digital signal: something like PCM sampling

Digital data:

        Analog signal: this is what modems generate

        Digital signal: we need some form of encoding.


Data: the original data format
Signal: the signal actually transmitted
Transmission: how we handle that signal on the wire.

analog v data v (encoding | transmission)

Note analog data / analog signal is an odd case.

See http://intronetworks.cs.luc.edu/current/html/links.html#encoding-and-framing as a reference on encoding of (short-haul) digital signals on a wire.

Signals v Transmission:

Normally these should match. Note special case of analog signal / digital transmission, which is taken to mean that the analog signal encodes a digital signal in a way that the repeater can decode and re-encode.


Transmission impairments


Attenuation

1. need strength for reception
    Ethernet problem with detecting collisions
2. need strength above noise level
3. attenuation increases with frequency, leading to distortion

"loading coils" in voice telephony: cut off frequencies outside of a desired range; tremendous out-of-band attenuation

attenuation measured in dB; dB per unit distance
Here is a graph from Stallings showing the relative attenuation of voice frequencies:

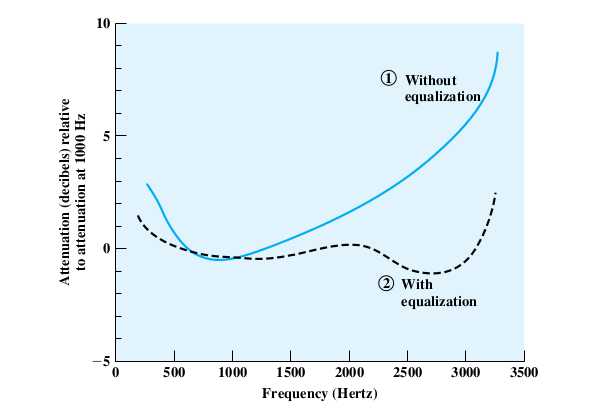
voice attenuation

Note use of equalization to make up for high-frequency loss


Brief review of decibels: logarithmic scale of relative power:
db = 10 log10 (P/Pbaseline)

3 dB   = 2Γ—    log10(2) = .30103
5 dB   = 3Γ—
7 dB   = 5Γ—  (5Γ— = 10Γ—/2Γ—; 7 = 10-3)
10 dB = 10Γ—
20 dB = 100Γ—

Attenuation problems 1 & 2 above can be addressed with amplification.
3rd problem introduces fundamental distortion; digitization solves this but analog equalization can work too.


Digital: high-frequency attenuation => signal degradation

Attenuation: leads to distortion of relative frequency strengths


Delay Distortion (like differential frequency attenuation, but different): different (sine) frequencies travel at different speeds.
Again, this leads to digital signal degradation, and some audio distortion.

Noise

Thermal noise:
N (watts) = kTB, B=band-width, T=temp, k=Boltzmann's constant (small!). Thermal noise is relevant for satellite transmission, but other sources of noise are usually more important for terrestrial transmission.
Note that thermal noise is proportional to the analog bandwidth; ie, it affects all frequencies identically.

It is often more convenient to use logarithms (base 10):

    Noise in dBW = log(k) + log(T) + log(B)

log(k) = -228.6 dBW

Suppose the temperature is 300K (27 degrees C) and the band-width is 20 MHz. Then the thermal noise is

    -228.6 + 10 log 300 + 10 log 20,000,000 = -228.6 + 24.8 + 73 = -133.5 dBW

dBW is the difference (in decibels) from a 1 Watt reference signal.

Intermodulation noise
This is the noise created by two signals interacting, in the same medium
Brief discussion on why it isn't universal.
Intermodulation noise requires some nonlinear interaction between the signals!
A linear combination of frequencies f1 and f2 (ie just transmitting them side-by-side in space) does not produce energy at f1+f2.

Crosstalk
Noise created by two signals interacting, on adjacent wires

Impulse noise
Interference (a form of impulse noise, from sharers of your frequency range)
Somebody else is using your frequency. Perhaps to make microwave popcorn. (Or perhaps you are simply driving around in the country listening to the radio.)

Other sources of noise:


Channel capacity

Nyquist's Theorem: the signal rate is the rate of sending data symbols. Nyquist's theorem states that

    maximum binary signal rate = 2 B

Where B is the width of the frequency band (that is, the "band-width").

This can be hard to realize in practice.

Signal rate v data rate: if we use binary signaling (binary encoding), then this means

    max data rate = 2 B         (binary version)

We might also send symbols (signal elements) each encoding L bits, in which case the data rate is LΓ—signal_rate. One way to do this is to use multi-level encoding, using M=2L distinct signal values (eg distinct amplitudes, etc). In this case we have

    max data rate = 2 B Γ— log2(M)          (multi-level version)

For binary signals, M=2 and log2(M)=1, so we just get the binary-version formula. Log2(M) is the number of bits needed to encode M, that is, the number of bits per symbol.

Signal rate is sometimes called "modulation rate". It is traditionally measured in baud. Note that for a 56k "baud" modem, it's the data rate that is 56kbps; the signaling rate is 8000/sec.

Compare Nyquist to the Sampling Theorem, which says that if a sine wave has frequency B, then it can be exactly reproduced if it is sampled at a rate of 2B. (Note: the sampling theorem allows for exact reproduction only if the sampled values are exact. In real life, the sampled values are digitized, and thus "rounded off"; this is called quantizing error.)

Basis of Nyquist's theorem: fundamental mathematics applied to individual sine waves.

The data rate is sometimes called "bandwidth" in non-analog settings.

The Nyquist limit does not take noise into account.

Note that if we are talking about a single sin(x), then analog band-width = 0! sin(x) does not carry any useful information.


Example 1: M=8, log2(M) = 3. Max data rate is 6B.

With M levels, we can carry log2(M) bits where we used to only carry 1 bit.


Why can't we just increase the bits per signal indefinitely, using multi-level encoding with more and more levels?
Answer: noise.

The Shannon-Hartley Theorem uses the noise level to give an upper bound on the communications throughput.

If S is the signal power and N is the noise power, then the signal-to-noise ratio, SNR, is S/N. This is often measured in dB, though in the formula below we want the actual ratio (25 dB = 300Γ—)

Shannon-Hartley claim:

    C ≀ B log2(SNR + 1)

where B = band-width, C = maximum channel capacity

Example: 3000Hz voice bandwidth, S/N = 30 dB, or a ratio of 1000.

    C = 3000*log2(1000) = 3000*10 = 30kbps

Note that increasing signal strength does tend to increase noise as well. Also, increasing band-width increases noise more or less in proportion. So: increasing B does lead to more thermal noise, and thus by Nyquist's formula SNR will decrease.


Here's a quick attempt to justify the Shannon-Hartley formula, borrowed from www.dsplog.com/2008/06/15/shannon-gaussian-channel-capacity-equation. It essentially derives Hartley's original formula. Let us start with the assumption that Sv is the maximum signal voltage, and Nv is the range of noise voltage; noise itself ranges from βˆ’Nv/2 to +Nv/2. Nv is much smaller than Sv. We'd like to choose an M so the M different voltages 0, Sv/(M-1), 2Sv/M, ..., (M-1)Sv/(M-1) are all distinct. This means that the step between two adjacent voltages is at least as large as Nv, as the upper voltage can have Nv/2 subtracted while the lower voltage can have Nv/2 added. This means Sv/(M-1) = Nv, or

    M = Sv/Nv+1 = (Sv+Nv)/Nv

The number of bits we can send with M levels is log2(M) = log2(Sv/Nv+1).

We're using voltages here; we really want to use power, which, all else being equal, is proportional to the square of the voltage. Let S = Sv2 and N = Nv2, so (S/N)1/2 = Sv/Nv.  We now have, ignoring the "+1" because S/N is large,

    log2M = (1/2) log2(S/N)

If B is the bandwidth then Nyquist's theorem says in effect that the maximum symbol rate is 2B. This means that our data rate is 2B Γ— (1/2) log2(S/N) = B log2(S/N).

We've said nothing about the idea that noise is statistically distributed following the Gaussian distribution. But this is a first step.


Let us equate the Shannon and Nyquist formulas for C:

C = 2B log2(M) ≀ B log2(SNR+1)
M2 ≀ SNR+1

Suppose we take SNR = 251Γ—; from the above we can infer that we can have at most M=16 signal levels.


56kbps modem: C=56kbps, B=3100Hz. C/B = 18
18 = log2(1 + SNR); SNR ~ 218 = 260,000 = 54 dB

Nyquist and 56Kbps modem: B=4kHz; 128 = 27 levels
Shannon and 28/56Kbps modems

Eb/N0

noise is proportional to bandwidth; let N0 = noise power per Hertz.
Eb = energy per bit of signal  (eg wattage of signal Γ— time-length of bit; this decreases with increased signaling rate (shorter time)) or lower average signal energy.
Ratio is Eb/N0

Note that this is a dimensionless quantity, though as a ratio of energy levels it is often expressed (logarithmically) in dB.

bit error rate decreases as this increases; significant for optical fiber designers

We will often assume N0 is all thermal noise, equated to kB, but the notion makes sense when there is other noise too.
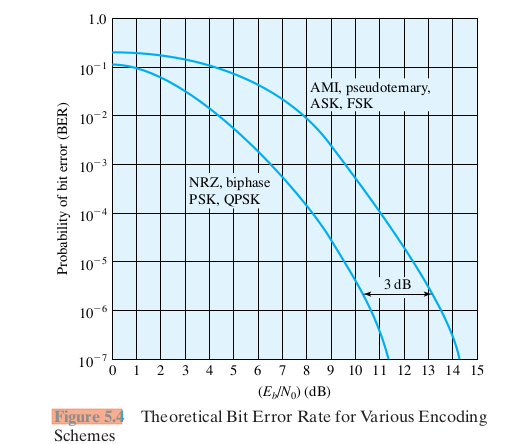
Here is figure 5.4 from Stallings involving BER v Eb/N0:


BER v Eb/No

Transmission Media


EM spectrum:
    10
    100
    1000        voice
    104
    105           
    106             AM radio
    107             shortwave
    108             FM radio, television
    109             Wi-Fi, microwave ovens
    1010            microwaves
    1011           
    1012         Low end of infrared
    1013
    1014         Red end of visible light

Attenuation of various media (from Stallings)


Twisted pair (loading coils)    0.2 dB/km at 1kHz
Twisted pair (voice-grade)    0.7 dB/km at 1kHz, 25 dB/km at 1 MHz
Cat-3                                      12 dB/km at 1 MHz
Coax                                        2dB/km at 1 MHz
Coax (fat)                                 7 dB/km at 10 MHz
Fiber                                       0.2 - 0.5 dB/km

consider attenuation & interference for the following.
Note: attenuation measured in dB/km! What are the implications of this!


At 16 mHz, attenuation per tenth of a km:
        13 dB (cat 3)
         8 dB (cat 5)  (80 dB/km)
   
    Why is it TWISTED??
   
summary: Coax has less attenuation, much less crosstalk/interference, but is $$


fiber
fiber modes
light source: lasers or LEDs (the latter is cheaper)


ADSL issues:
Stallings table 4.2: Cat-3 twisted pair has an attenuation of 2.6dB/100m!! (at 1 mHz)
Over the maximum run of 5 km, this works out to an incredible 90dB loss! And residential phone lines are not twisted-pair.
384Kbps: 17,000 feet
1.5mbps: 12,000 feet
ADSL must deal with tremendous signal attenuation!
Thermal noise becomes very serious!

Antennas

Satellite note: I used to have satellite internet.
My transmitter was 2 watts. This reached 23,000 miles.

The central problem with satellite phone (and internet) links is delay. The round-trip distance (up-down-up-down) is 4x23,000 miles, for a minimum propagation delay of 495 ms. For Internet, there was usually an additional 500 ms of queuing delay.

Frequencies: < 1.0 gHz: noisy
> 10  gHz: atmospheric attenuation
Wi-fi uses the so-called "ISM" band, at around 2.4 gHz

4.3: propagation
High-frequency is line-of-sight, but low frequency (<= ~ 1 mHz) bends
In between is "sky-wave" or ionospheric skip (2-30mHz)

Once upon a time, AT&T had chains of microwave towers, 40-50 miles apart. They would relay phone calls. They're obsolete now, replaced by fiber. The concrete tower in the picture below, built in 1950, is the original phone microwave-relay tower; the newer steel tower arrived in 1957. (Further information about this particular site can be found at long-lines.net/places-routes/LeeIL; information about the entire system can be found at long-lines.net.) The single-story base building is huge; it was built to house vacuum-tube electronics and early transistor technology. Nowadays the electronics fit within the base of each antenna.

old ATT microwave-relay tower

Suppose you could have 100 mHz of band width (eg 2.5-2.6 gHz). At 4 kHz per call, that works out to 25,000 calls. That many calls, at 64kbps each, requires a 1.6-gbit fiber line. In the SONET hierarchy, that just below OC-36/STS-36/STM-12. Single fiber lines of up to STM-1024 (160 Gbps; almost 100 times the bandwidth) are standard, and are usually installed in multiples.

Is it cheaper to bury 50 miles of cable, or build one tower?

Now suppose you decide (before construction begins) that you need 10Γ— more capacity. What then?

Line-of-sight:

Attenuation, inverse-square v exponential

water vapor: peak attenuation at 22gHz (a 2.4gHz microwave is not "tuned" to water)
rain: scattering
oxygen: peak absorption at 60 gHz

cell phones: 824-849mhz
pcs: 1.9ghz

Attenuation along a wire (coax, twisted pair, or anything else) is exponential, while wireless attenuation is proportional to the square of the distance, meaning that in the long run wire attenuation becomes much more significant than wireless.

Every time you double the distance with wireless, the signal strength goes down by a factor of 4, which is a 6 dB loss. Suppose a cable has a loss of 3 dB per 100 m (factor of 2). Suppose the wired signal is 10 db ahead at 100 m. We get the following

distance wired wireless
100 m 0 db -10 db
200 m -3 db -16 db
400 m -9 db -22 db
800 m -21 db -28 db
1600 m -45 db -34 db

Starlight (a form of wireless) is detectable at distances of 100's of light-years.

Techniques for Modulation and Encoding

5.1  digital data/digital signal

NRZ is the "simple" encoding. But on short-haul links it has problems with clock drift. It has additional problems with long-haul encodings.

See also http://intronetworks.cs.luc.edu/current/html/links.html#encoding-and-framing about the encoding of short-haul digital signals on a wire.


data rate v modulation rate: these are often not the same
(ethernet: data rate 10Mbps, modulation rate 20Mbaud)
phone modems: data rate 56kbps, modulation rate 7kbaud

RZ, NRZ

    issues:
        clocking
        analog band width: avoid needing waveforms that are too square
        DC component (long distances don't like this)
        noise
       
             
NRZ flavors
inversion (NRZ-I) v levels (NRZ-L)
differential coding (inversion) may be easier to detect than comparison to reference level
Also, NRZ-I guarantees that long runs of 1's are self-clocked
Problems:
DC component: non-issue with short (LAN) lines, larger issue with long lines
losing count / clocking (note that NRZ-I avoids this for 1's)

Requirements:
bipolar (bipolar-AMI): 1's are alternating +/-; 0's are 0
    Fixes DC problem! Still 0-clocking problem
   
Note that bipolar involves three levels: 0, -1, and +1.

biphase: (bi = signal + clock)
Example: Manchester (10mbps ethernet)
    10mbps bit rate
    20mbps baud rate (modulation rate)

bipolar-8-zeros (B8ZS)

This is what is used on most North American T1 lines (I'm not sure about T3, but probably there too)

1-bits are still alternating +/-; 0-bits are 0 mostly.
If a bytes is 0, that is, all the bits are 0s (0000 0000), we replace it with 000A B0BA, where A = sign of previous pulse and B=-A.
This sequence has two code violations. The receiver detects these code violations & replaces the byte with 0x00.
Note the lack of a DC component

Example: decoding a signal

Bipolar-HDB3: 4-bit version of B8ZS


4b/5b

4-bit data
 5-bit code
0000  
11110
0001  
01001
0010  
10100
0011  
10101
...
1100  
11010
1101  
11011
1110  
11100
1111  
11101
IDLE  
11111
DEAD  
00000
HALT  
00100
        
        
4b/5b involves binary levels, unlike bipolar. It does entail a 20% reduction in the data rate.

It is used in 100-mbit Ethernet



Fig 5.3 (8th, 9th edition): spectral density of encodings. Spectral density refers to the band-width that the signal needs.

Lowest to highest:
  1. biphase (Manchester, etc)
  2. AMI,
  3. B8ZS
Latter is narrower because it guarantees more transitions
=> more consistent frequency

Fig 5.4: theoretical bit error rate
biphase is 3 dB better than AMI: not sure why. This means that, for the same bit error rate, biphase can use half the power per bit.



HDLC Bit Stuffing


The HDLC protocol sends frames back-to-back on a serial line; frames are separated by the special bit-pattern 01111110 = 0x7E. This is, however, an ordinary byte; we need to make sure that it does not appear as data. To do that, the bit stuffing technique is used: as the sender sends bits, it inserts an extra 0-bit after every 5 data bits. Thus the pattern 01111110 in data would be sent as 011111010. Here is a longer example:

data:        0111101111101111110
sent as:    011110111110011111010

The receiver then monitors for a run of 5 1-bits; if the next bit is 0 then it is removed (it is a stuffed bit); if it is a 1 then it must be part of the start/stop symbol 01111110.

Some consequences:
  1. We have guaranteed a maximum run of 6 1-bits; if we interchange 0's and 1's and use NRZ-I, bit-stuffing has solved the clocking problem for us.
  2. The transmitted size of an HDLC data unit depends on the particular data, because the presence of stuffed bits depends on the particular data. This will ruin any exact synchronization we had counted on; for example, we cannot use HDLC bit-stuffing to encode voice bytes in a DS0 line because the extra stuffed bits will throw off the 64000-bps rate.
  3. The data sent, and the 01111110 start/stop symbol, may no longer align on any byte boundaries in the underlying transmission bitstream.
see also http://intronetworks.cs.luc.edu/current/html/links.html#framing.


Analog data / Digital signal

(Stallings 5.3)

sampling theorem: need to sample at twice the max frequency, but not more

basic idea of PCM: we sample at regular intervals (eg 1/8000 sec), digitize the sample amplitude, and send that.

PCM stands for Pulse Code Modulation; it replaced an earlier analog strategy called PAM: Pulse Amplitude Modulation. In PAM, the signal was sampled and then a brief carrier pulse of that amplitude was sent. This is a little like AM, except the pulses could be short, and time-division-multiplexed (below) with other voice channels. The C in PCM means that the analog signal was replaced by a "code" representing its amplitude. This is all meant to explain why digital sampling, which is what PCM is, gets the word "modulation" in its name, which is really not applicable.

In the early days, one sampler (PCM encoder) could sample multiple analog input lines, saving money on electronics.

sampling error v quantization error
nonlinear encoding versus "companding" (compression/expansion)
   
The voice-grade encoding used in the US is known as πœ‡-law (mu-law) encoding; πœ‡ is a constant used in the scaling formula, set equal to 255. We define F(x) as follows, for -1<=x<=1 (sgn(x) = +1 for x>0 and -1 for x<0):

    F(x) = sgn(x)*log(1+πœ‡*|x|) / log(1+πœ‡),

Note that for -1<=x<=1 we also have -1<=F(x)<=1. If x is the signal level, on a -1≀x≀1 scale, then F(x) is what we actually transmit. More precisely, we transmit 128*F(x), rounded off to the nearest 8-bit integer. The use of F(x) has the effect of nonlinear scaling, meaning that for x close to 0 there are still a wide range of levels. Consider the following few values:
   
    F(1)=1, F(-1)=-1, F(0)=0
    F(0.5)= .876,      Γ— 128 = 112
    F(0.1)= .591       Γ— 128 = 76
    F(0.01)= .228     Γ— 128 = 29
    F(0.001)= .041   Γ— 128 =  5

These last values mean that faint signals (eg, x = 0.001) still get transmitted with reasonably limited quantizing roundoff. A signal around x = 0.01 can get rounded off by at most 1/2Γ—29 ≃ 0.016; a signal around x = 0.001 gets rounded off by at most 1/2Γ—5 = 0.1. With linear scaling, a signal level of 0.01 (relative to the maximum) would encode as 1 (0.01 Γ— 128 = 1.28 ≃ 1), and anything fainter would round off to 0.

This is often called companding, for compression/expanding; note that it is done at the per-sample level. If everyone's voice energy ranged, say, from 100% down to a floor of 20% of the maximum, companding wouldn't add anything. But voice energy in fact has a much wider dynamic range.

Music, of course, has an even larger dynamic range, but musical encoding almost always uses 16 bits for sampling, meaning that plain linear encoding can accurately capture a range from 100% down to at least 0.1%. 8-bit πœ‡-law companding is often considered to be about as accurate, from the ear's perspective, as 12 or 13-bit linear encoding.

Demo of what happens if you play a πœ‡-law-encoded file without the necessary expansion: faint signals (including hiss and static) get greatly amplified. To get sox to accept this, rename cantdo.ulaw to cantdo.raw and then:

    play -r 8000 -b 8 -c 1 -e signed-integer cantdo.raw

A-law encoding: slightly different formula, used in Europe.

By comparison to companding, compression may involve taking advantage of similarities in a sequence of samples. MP3 is a form of true compression, though it is not used in telephony (because it is hard to do in real time). G.729 is a high-performance form of true compression frequently used in voice.

delta modulation: This involves encoding the data as a sequence of bits, +1 or -1. The signal level moves up by 1 or down by 1, respectively. This limits how closely the encoded signal can track the actual signal. I have no idea if this is actually used. It has a bias against higher frequencies, which is ok for voice but not data
advantage: one bit! However, higher sampling rates are often necessary.

Performance of digital voice encoding:
voice starts out as a 4kHz band-width.
7-bit sampling at 8kHz gets 56kbps, needs 28kHz analog band-width (by Nyquist)
(Well, that assumes binary encoding....)
BUT: we get voice: often analog=>digital, then encoded as analog signal on the transmission lines!

Analog data / Analog signal

(Stallings 5.4)
Why modulate at all? The primary reasons are

AM and FM radio is the classic example. Cellular telephony would be analog data / digital signal


The simplest is AM.
AM band-width usage is worth noting
new frequencies at carrier +/- signal are generated because of nonlinear interaction (the modulation process itself).

Single Side Band (SSB): slightly more complex to generate and receive, but:
Sound files: beats.wav v modulate.wav
Latter has nonlinearities

(1+sin(sx)) sin(fx)  = sin(fx) + sin(sx)sin(fx)
        = sin(fx) + 0.5 cos((f-s))x) - 0.5 cos((f+s)x)

reconsider "intermodulation noise". This is nonlinear interactions between signals, which is exactly what modulation here is all about.

Angle Modulation (FM and PM)

FM is Frequency Modulation; PM is Phase Modulation. These can be hard to tell apart, visually.
Let m(t) = modulation signal (eg voice or mustic).
The (transmitted) signal is then

    A cos (2πœ‹ft + πœ‘(t))

FM: k*m(t) = πœ‘'(t) (that is, πœ‘(t) = ∫m(t)dt). If m(t) = c is constant for an interval, then πœ‘(t) = kct = k1t; that is, we have the transmitted signal as

    A cos (2πœ‹ft + kct) = A cos (2πœ‹(f+kc/2πœ‹) t),

a signal with the fixed (higher) frequency f+kc/2πœ‹.

(We are assuming m(t) is a constant level, not a constant frequency)

PM: k*m(t) = πœ‘(t).  m(t) = const => πœ‘(t) = const. We shift phase for the duration of the constant interval, but the base frequency changes only when m(t) is changing.

See modulation.xls.


Somewhat surprisingly, FM and PM often sound very similar. One reason for this is that the derivative (and so the antiderivative) of a sine wave is also a sine wave. There's distortion in terms of frequency, but most voice frequencies are in a narrow range.

Picture: consider a signal m(t) = 0 0 1 1 1 1 1 1 0 0 0 0
FM,PM both need more band-width than AM
AM:    band-width = 2B, B=band-width of orig signal

FM,PM: band-width = 2(Ξ²+1)B, where again B = band-width of original signal. This is Carson's Rule.

For PM, Ξ² = npAmax, A_max = max value of m(t) and np is the "phase modulation index", a quantity proportional to k in the PM rule k*m(t) = πœ‘(t).

For FM, Ξ² =  𝚫F/B, 𝚫F = peak frequency difference. A value of Ξ²=2, for example, would mean that in encoding an audio signal with band-width 4 KHz, the modulated signal varied in frequency by a total range of 8 KHz. Having Ξ² low reduces the band-width requirement, but also increases noise. Also note that in our Ξ²=2, the total band-width needed for the modulated signal wold be 24 KHz.

Digital data / Analog signal

Stallings 5.2

modems, long lines & fiber

(even long copper lines tend to work better with analog signals)

ASK: AM modulation using something like the NRZ signal as the input. It is a "naive" encoding, though used for fiber

FSK: FM modulation. 1-bits are transmitted by brief pulses at frequency f1 (that is, A cos(2πœ‹f1t)), while 0-bits are transmitted by brief pulses at another frequency f2. The bit-time must be long enough that the two frequencies f1 and f2 are easily distinguished!

On optical fiber, FSK is represented by color shift.

PSK: easier to implement (electrically) than FSK. 0-bits might be sent as A cos(2πœ‹ft), while for 1-bits the waveform might change to A cos(2πœ‹ft + πœƒ)

Superficially, ASK appears to have zero analog band-width, but this is not really the case!

ASK: 1 bit /hertz => 4000 bps max over voice line

1 bit/ 2Hz, 2400 Hz carrier => 1200 bps.



FSK analog band-width = high_freq - low_freq

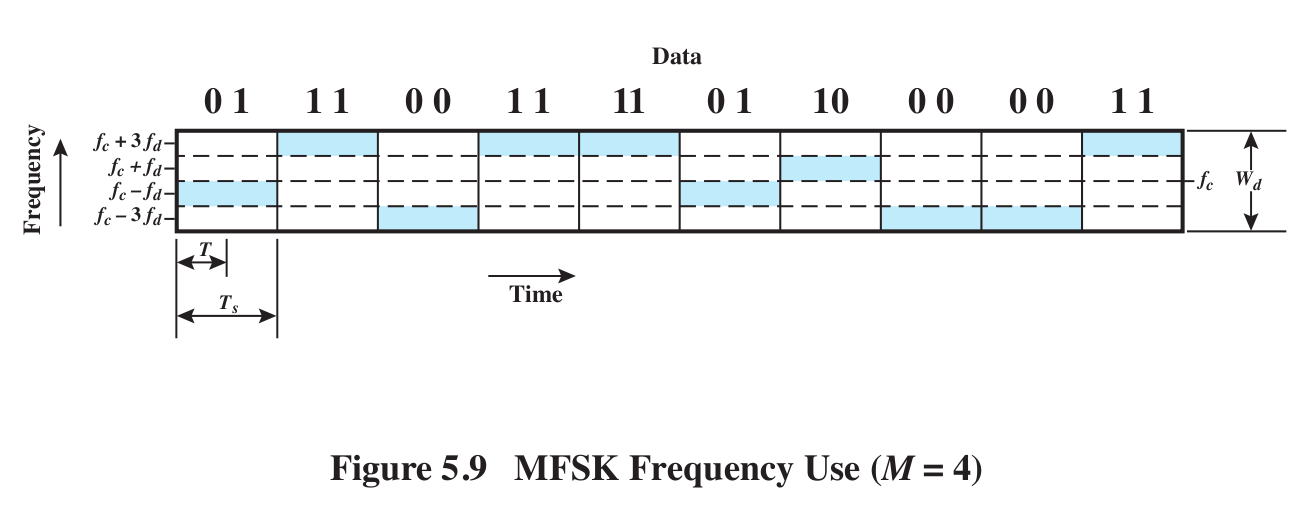
MFSK: we use multiple frequencies to send several bits at once. If we have four frequencies to use (eg f-3d, f-d, f+d and f+3d, where f is the "carrier"), then one frequency encodes two bits. We might even label the frequencies with the bits encoded: f00, f01, f10, f11.

BFSK v MFSK: fig 5.9 for MFSK.

diagram of MFSK

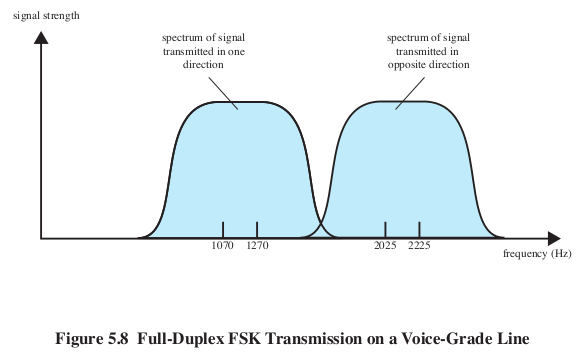
BFSK: fig 5.8: old modems, full-duplex
One direction of the signal might use the frequency band 600-1600 Hz, and the other direction might use the band 1800-2800 Hz.

MFSK: the trouble is, it takes time to recognize a frequency (several cycles at least!)

FSK is supposedly more "noise-resistant" than ASK, but fig 5.4 shows the same graph of Eb/N0 v BER for the two. (PSK is shown 3 dB lower (better) in the graph)

graphs


BPSK: decoding starts to get very nonintuitive!

DPSK: differential, like differential NRZ

QPSK: 4 phase choices, encoding 00, 01, 10, 11
9600bps modem: really 2400 baud; 4 bits per signal element (12 phase angles, four of which have two amplitude values, total 16 distinct values per signal, or 4 bits)


Nyquist limit applies to modulation rate: noise reduces it.

56Kbps modems: use PCM directly.
Station gets data 7 bits at a time, every 1/8 ms, and sets the output level to one of 128 values.

If there is too much noise for the receiver to distinguish all those values, then use just every other value: 64 values, conveying 6 bits, for 48kbps. Or 32 values (using every fourth level), for 5*8 = 40 kbps.


Quadrature Amplitude Modulation, QAM

This involves two separate signals, sent 90Β° out of phase and each amplitude-modulated (ASK) separately. Because the two carriers are 90Β° out of phase (eg sin(ft) and cos(ft)), the combined signal can be accurately decoded.

We will ignore the QAM details.



An Example

The following example is due to Oona RΓ€isΓ€nen, via her blog at windytan.com/2014/02/mystery-signal-from-helicopter.html. We make use of audacity and the SoX program.

We start with a police helicopter video at youtube.com/watch?v=TCKRe4jJ0Qk. What is that buzzing noise? The engine? Step 0 is to save the sound track as an mp3 file (police_chase.mp3), using, say, vidtomp3.com.

Next, using Audacity, convert the mp3 file to .wav format. While we're here, note the distinctive appearance of the left channel.

The next step is to extract the left channel using

    sox police_chase.wav -c 1 left.wav remix 1

Zoom in on the left.wav file. It appears to be a mixture of higher-frequency and lower-frequency sine waves. The high-frequency wavelength is about .45 ms, making the frequency ~2200 Hz; the lower-frequency wavelength is about .85 ms, making the frequency ~1200 Hz. These numbers turn out to match the Bell 202 modulation scheme, which uses FSK: data is sent at a rate of 1200 bps, with 1-bits encoded as a single wavelength at 1200 Hz and 0-bits encoded as 1.83 wavelengths (1/1200 sec) at 2200 Hz. Bell 202 modulation is still used to transmit CallerID data to analog landline phones.

How do we demodulate the signal? One approach is to apply lowpass and highpass filters about the midpoint, 1700 Hz, and compare the outputs:

    sox left.wav hi.wav sinc 1700
    sox left.wav lo.wav sinc -1700

Combine the two channels:

    sox --combine merge lo.wav hi.wav both.wav remix 1 2

and look at the two signals side-by-side. To demodulate, we'd need to do the following:

An easier way to demodulate is to use minimodem:

    minimodem --receive 1200 -f left.wav | tr '\200-\377\r' '\000-\177\n'

The "tr" (translate) command unsets the high-order bit to get 7-bit ascii, with \n replacing \r.

This gives us latitude and longitude coordinates that match up fairly well with the path of the helicopter! Consider the first data point:

    N390386 W0943420

This appears to be in "decimal minutes" format:

    39 3.86, -94 34.20

Rules for entering latitude and longitude into maps.google.com are at support.google.com/maps/answer/18539.

The video itself starts at 39Β°03'51.6"N 94Β°34'12.0"W, at the corner of Volker Blvd and Troost Ave; this is almost two miles due south of the coordinates above.

The Swope Parkway Tennis Courts are at 39Β°02'28.9"N 94Β°33'43.7"W. In the video we pass these at T=17 sec; the helicopter is looking south and the car is heading east, about to head under I-71.

The video has 1428 seconds and the telemetry data has 5706 lines, for just about exactly 4 lines (2 position records) a second. At T=3:30 (210 seconds) the car is at the intersection of I-71 and 39th street. That's line 840 of the file, where the coordinates are N390269 W0943368. If we plot that on google maps, as 39 2.69, -94 33.68, we get I-71 and 45st street; the helicopter is now "only" six blocks behind.

(Note that the telemetry sound fluctuates twice a second; that is, once per record! At 1200 bits/sec, we can send 150 bytes/sec. The actual position records are ~48 bytes long, with null bytes added to take up the slack.

MULTIPLEXING

Brief note on synchronous v asynchronous transmission

Sender and receiver clocks MUST resynchronize at times; otherwise, the clock drift will eventually result in missed or added bits.

Asynchronous: resynchronise before/after data, eg with a "stop bit" before and after each byte. This is common approach with serial lines, eg to modems.

Synchronous: send data in blocks too big to wait to resynchronize at the end, but embed synchronization in the data (with NRZ-I, for example, we usually resynchronize on each 1-bit).

Manchester (a form of synchronous): we interleave clock transitions with data transitions.

More efficient techniques make sure there are enough 1's scattered in the data itself to allow synchronization without added transitions. Example: 4b/5b: every 5 bits has at least 2 transitions (2 1-bits)


Brief note on PACKETs as a form of multiplexing

The IP model, with relatively large (20 byte for IP) headers that contain full delivery information, is an approach allowing a large and heterogeneous network. But simpler models exist.

The fundamental idea of packets, though, is that each packet has some kind of destination address attached to it. Note that this may not happen on some point-to-point links where the receiver is unambiguous, though what "flow" the packet is part of may still need to be specified.

HDLC packet format: omit

Voice channels

The basic unit of telephony infrastructure is the voice channel, either a 4 KHz analog channel or a 64 kbps DS0 line. A channel here is the line between two adjacent switching centers; we might also call them channel segments. An end-to-end voice path is a sequence of channels. To complete a call, we do two things:
  1. reserve an end-to-end sequence of voice channels for the call
  2. at each switch along the way, arrange for the output of a channel to be forwarded (switched) to the next channel in the path.
Channels are either end-user lines or are trunk channels; the latter are channels from one switching center to the next. Within the system, channels are identified by their Circuit Identification Code. It is the job of Signaling System 7 (in particular, the ISDN User Part, or ISUP, of SS7, to handle the two steps above). The spelling "signalling" is common in this context. SS7 also involves conveying information such as caller-ID and billing information.

Note that VoIP does not involve anything like channels; we just send packets until a link is saturated. The channel-based system amounts to a hard bandwidth reservation (with hard delay bounds!) for every call.

The channel is the logical descendant of the physical circuit. At one point, the phone system needed one wire per call. Channels allow the concept of multiplexing: running multiple channels over a single cable. We'll now look at three ways of doing this:
More on the signaling and switching processes below

FDM (Frequency Division Multiplexing)

AM radio is sort of the archetypal example. This is a fundamentally analog technique, though we can use FDM and digital data (eg ASK or FSK).


ATT "L-carrier" FDM
voice example
4kHz slots; 3.1kHz actual bandwidth (300 Hz - 3400 Hz). AM SSB (upper sideband) modulation onto a carrier frequency f transforms this band into the band [f, f+4kHz], of the same width. Note that without SSB, we'd need double the width; FM would also use much more bandwidth than the original 4kHz.

L-carrier frequency diagram

ATT group/supergroup hierarchy: Table 8.1

name
 composition
 # channels
Group
12
Supergroup
 5 groups
 5 Γ— 12 = 60
Mastergroup
 10 supergroups
 10 Γ— 60 = 600
Jumbogroup
 6 mastergoups
 6 Γ— 600 = 3600
Mastergroup Multiplex
 N mastergroups
 N Γ— 600

L-carrier: used up through early 1970s

Why bundle calls into a hierarchy of groups? So you can multiplex whole trunks onto one another, without demuxing individual calls. Peeling out a single call is relatively expensive, particularly if we want to replace that slot with a new call. For one thing, additional noise is introduced.

Even the repeated modulation into larger and larger groups introduces noise.



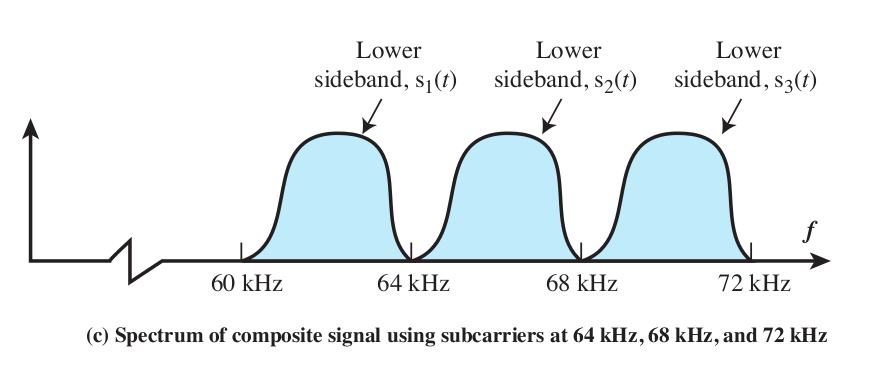
Brief comparison of Stallings Fig 5-8 (below) and Fig 8-5 (above). Both show side-by-side bands, interfering minimally. The first is of two bands in the voicerange (1 kHz and 2 kHz respectively), representing a modem sending in opposite directions. The second is of multiple 4 kHz voice bandsAM-modulated (using SSB) onto carriers of 60 kHz, 64 kHz, 68 kHz, ....

modem channels