Comp 346/488: Intro to Telecommunications

Tuesdays 4:15-6:45, Lewis Towers 412

Class 11, Apr 3

    Chapter 11, ATM
    Chapter 13, congestion control (despite the title, essentially all the detailed information is ATM-specific)
    Chapter 14, cellular telephony


Spread Spectrum

9.2: FHSS & Hedy Lamarr / George Antheil

Both sides generate the same PseudoNoise [PN] sequence. The carrier frequency jumps around according to PN sequence.
In Lamarr's version, player-piano technology would have managed this; analog data was used. Lamarr's intent was to avoid radio eavesdropping (during WWII); an eavesdropper wouldn't be able to guess the PN sequence and thus would only hear isolated snippets.

Here's a colorized version of Stallings fig 9.4. The PN sequence chooses the appropriate broad color band; the four possible values of a data symbol choose one of the four sub-bands within a broad colored band.

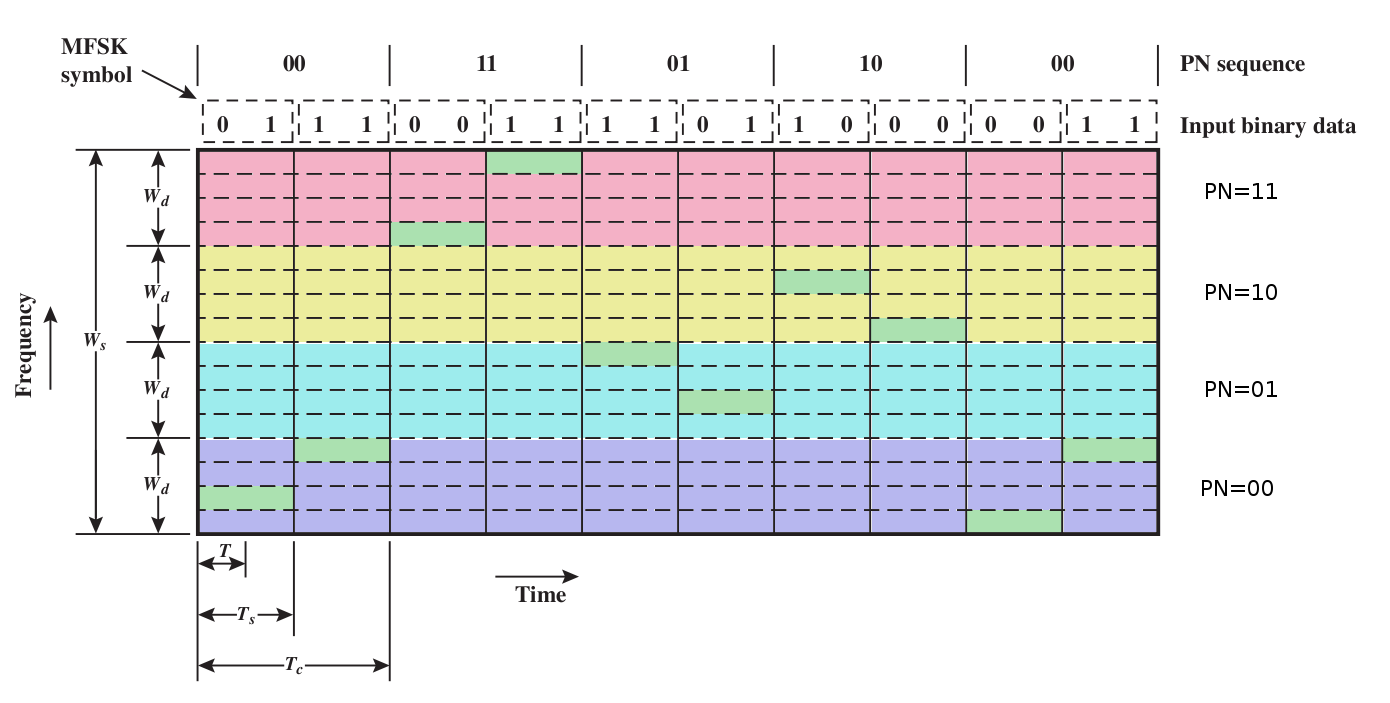
FHSS

FHSS
We will use a "pseudo-noise" or pseudo-random (PN) sequence to spread the frequencies of MFSK over multiple "blocks"; each MFSK instance uses one block. Each endpoint can compute the PN sequence, but to the world in between it appears random. For each distinct PN symbol we will use a band like the MFSK band above, but we'll have multiple such bands all stacked together, a different band for each distinct PN symbol.
Tc: time for each unit in the PN sequence
Ts: time to send one block of L bits

slow v fast FHSS/MFSK: Fig 9.4 v 9.5
slow: Tc >= Ts: send >= 1 block of bits for each PN tick
fast: Tc < Ts: use >1 PN tick to send each block of bits

feature of fast: we use two or more frequencies to transmit each symbol; if there's interference on one frequency, we're still good.

Consider 1 symbol = 1 bit case

If we use three or more frequencies/symbol, we can resolve errors with "voting"

What is this costing us?


9.3: Direct-Sequence Spread Spectrum (DSSS)

Each bit in original becomes multiple bits, or chips. We end up using a lot more bandwidth for the same amount of information! The purpose: resistance to static and interference (especially multipath interference).

Same spreading concept as fast FHSS, but stranger.

Basically we modulate the signal much "faster", which spreads the bandwidth as a natural consequence of modulation. We no longer have a discrete set of "channels" to use.

Suppose we want to use n-bit spreading. Each side, as before, has access to the same PN sequence. To send a data bit, we do the following:
Note that we are transmitting n bits in order to communicate one bit. The receiver then:
See Figure 9.6.

For every data bit, we will actually receive n bits. Those n bits, XORed with the appropriate n bits from the PN sequence, should give either n 0-bits or n 1-bits. A few wrong bits won't matter; we can simply go with the majority.

Recall that AM band width was proportional to the band width of the signal. The same thing is happening here: if sending the data 1 bit at a time needed a band width of B, then sending n bits at a time will likely need a band width of about nB. Thus, like FHSS, we've greatly expanded the band width requirement.

Sometimes it is easier to think of the signal as taking on values +1 and -1, rather than 0/1. Then, we can multiply the data bit by the n-bit PN sequence; multiplication by -1 has the effect of inverting.

Figure 9.9 shows the resultant spectrum. Because we're sending at a n-times-faster signaling rate, our spectrum is also n times wider. Why would we want that? Because jamming noise is likely to be isolated to a small part of the frequency range; after the decoding process, the jamming power is proportionally less.

9.4:  CDMA

Here, each sending channel is assigned a k-bit chipping code; each data bit becomes k "chips" (k is often ~128, though in our examples we'll use k=4 or k=6); these replace the PN sequence (mostly; see below). Each receiver has the corresponding chipping code. The chips are sent using FHSS or DSSS; for DSSS, the sender sendsthe chipping code for a 0-bit and the inverted chipping code for a 1-bit.

As with FHSS and DSSS, one consequence is that data is spread out over a range of frequencies, each with low power.

Unlike these, however, we are now going to allow multiple transmissions simultaneously, at least in the forward (tower to cellphones) direction. The signals to each phone, each with a unique chipping code, are added together and transmitted together; the receivers need to pick their own data bit out of the chaos.

basic ideas:

chipping codes: These are the sequences of k bits that we give each user, eg ⟨1,0,1,1,0,0⟩.

The algebra is more tractable if we instead treat 0 as -1, so the code above would become ⟨1,-1,1,1,-1,-1⟩.

dot product: Given two sequences of numbers A = ⟨a1,a2,a3,a4,a5⟩ and B = ⟨b1,b2,b3,b4,b5⟩, the dot product, or inner product, is
    A·B = a1*b1 + a2*b2 + a3*b3 + a4*b4 + a5*b5
If our sequences represent vectors in 3-dimensional space (that is, the sequences have length 3), then A·B=0 if and only if A and B are perpendicular, or orthogonal. Suppose we have some pairwise-orthogonal sequences, say A, B, C, and D, of any dimension (length); that is, A·B = B·C = A·C = A·D = B·D = C·D = 0; any two are perpendicular. Then, if we're given a vector E = a*A + b*B + c*C + d*D (where a,b,c,d are ordinary real numbers; multiplying a vector by a real number just means multiplying each component by that number: 2*⟨3,5,7⟩ = ⟨6,10,14⟩), we can immediately solve for a,b,c,d, regardless of our geometrical interpretation:
    E = a*A + b*B + c*C + d*D
    E·A = a*A·A + b*B·A + c*C·A + d*D·A
           = a*A·A     (because B·A = C·A = D·A = 0)
and so a = E·A / A·A. Similarly we can recover b, c and d. Usually we'll scale each of the A,B,C,D so A·A = 1, so a = A·E. (We don't do this below, so A·A = 6.)

The simplest set of orthogonal vectors, or chipping codes, is  ⟨1,0,0,0,0,0⟩, ⟨0,1,0,0,0,0⟩, ⟨0,0,1,0,0,0⟩, etc. But it's not the only set, as we'll see below.

Suppose we have K users wanting to transmit using CDMA. Each user will be given a vector of 0's and 1's (or -1's and 1's, depending on our perspective) of length k; this is the user's chipping code. Each user transmits k "chips" on k frequencies at the same time. Ideally we use K=k, but in practice K can be rather larger. All the transmissions add together, linearly (actually, we'll have to adjust the individual cellphone power levels so that, at the base antenna, all the signals have about the same power). The transmissions are done in such a way that the receiver can extract each individual signal, even though all the signals overlap. Similarly, when the base station wants to transmit to all K users, combines all K bits for each of k positions and transmits the whole mess; each individual receiver can extract its own signal.

Trivial way to do this: ith sender sends on frequency i only, and does nothing on other frequencies. This is just FDM, corresponding to the chipping codes ⟨1,0,0,0,0,0⟩, ⟨0,1,0,0,0,0⟩, ⟨0,0,1,0,0,0⟩, etc. We don't want to use this, though.

Example from Table 9.1:
codeA
  1
 -1
 -1
  1
 -1
  1
codeB
  1
 1
 -1
 -1
  1
  1
codeC
  1
  1
 -1
  1
  1
 -1

codeA∙codeB = 0, codeA∙codeC = 0, codeB∙codeC = 2 (using ∙ for "dot product")

userA sends (+1)*codeA or (-1)*codeA

suppose D = data = a*codeA + b*codeB, a,b = ±1

Then D∙codeA = a*codeA∙codeA + b*codeB∙codeA = a*6 + b*0 = 6a; we have recovered A's bit!
Similarly D·codeB = a*codeA·codeB + b*codeB·codeB = a*0 + b*6 = 6b, and we have recovered B's bit!

Now suppose the transmission D = -1*codeA + 1*codeB + 1*codeC. Can we recover the respective -1, 1 and 1?

combined data D
 1
 3
 -1
 -1
 3
 -1
codeA
 1
 -1
 -1
 1
 -1
 1
products w D
 1
 -3
 1
 -1
 -3
 -1
 sum = -6
codeB
 1
 1
 -1
 -1
 1
 1
products w D
 1
 3
 1
 1
 3
 -1
 sum = 8
codeC
 1
 1
 -1
 1
 1
 -1
products w D
 1
 3
 1
 -1
 3
 1
 sum = 8

Algebraically, D·codeA = -1*codeA·codeA = -6, because codeA is orthogonal to codeB and codeC
D·codeB = -1*codeA·codeB + 1*codeB·codeB + 1*codeC·codeB = -1*0 + 1*6 + 1*2 = 8. codeB and codeC are not orthogonal but they are "close"; codeB·codeC is "small" relative to 6.
Similarly, D·codeC = -1*codeA·codeC + 1*codeB·codeC + 1*codeC·codeC = -1*0 + 1*2 + 1*6 = 8.

Whenever codeB and codeC appear in the mix, we'll have an extra ±2 in the mix. But the expected answer is -6, 0, or 6, so if we round to the nearest such value we'll get the correct result.

Cell phones

analog
The AMPS standard used FDMA (Freq Division Multiple Access): allocates a 30kHz channel to each call (2 channels!), held for duration of call.

TDMA
digitizes voice, compresses it 3x, and then uses TDM to send 3 calls over one 30kHz channel.

GSM
form of TDMA with smaller cells, more dynamic allocation of cells. Note that if everyone talks at once, there might not be enough cells for all!  Data form: GPRS (General Packet Radio Service)

CDMA
sprint PCS, US Cellular, others
code division multiple access: kind of weird. This is a form of "spread spectrum". Signals are encoded, and spread throughout the band. Any one bit is sent as ~128 "chips", but chips may be used by multiple senders. Demultiplexing is achieved because codes are "orthogonal", as above.

This strategy may give good gradual degradation as the number of calls increases (assuming suitable chipping codes can be found), and good eavesdropping prevention (though not as good as strong encryption). It also gives excellent bandwidth utilization.

Note that we can only use this orthogonal-chipping-code strategy in the forward direction (tower to cellphones); for orthogonal codes to work, all the transmissions must be precisely synchronized. In the reverse direction, we might have had all the cellphones obey some synchronization protocol, but we don't; instead of orthogonal codes we use pseudorandom sequences. Given two random sequences A and B, of length N, the inner product A·B is typically 0.8*sqrt(N) (unless A=B, in which case A·B = N). We can't have N cellphones transmit simultaneously and expect the antenna to decode, but we can have sqrt(N), and furthermore the phones do not have to be synchronized in any way.

There is some debate about exactly why CDMA works better than TDMA; theoretically, bandwidth use should be the same. However, the big wins for CDMA appear to be in avoiding multipath distortion and in frequency reuse in neighboring cells. If one or two frequencies are affected by multipath (which is usually very frequency-dependent), the other frequencies over which CDMA spreads the signal can take up the slack.

Here is Stallings figure 14.2 (at least the N=4 and N=7 cases; the book also illustrates a N=19 example).
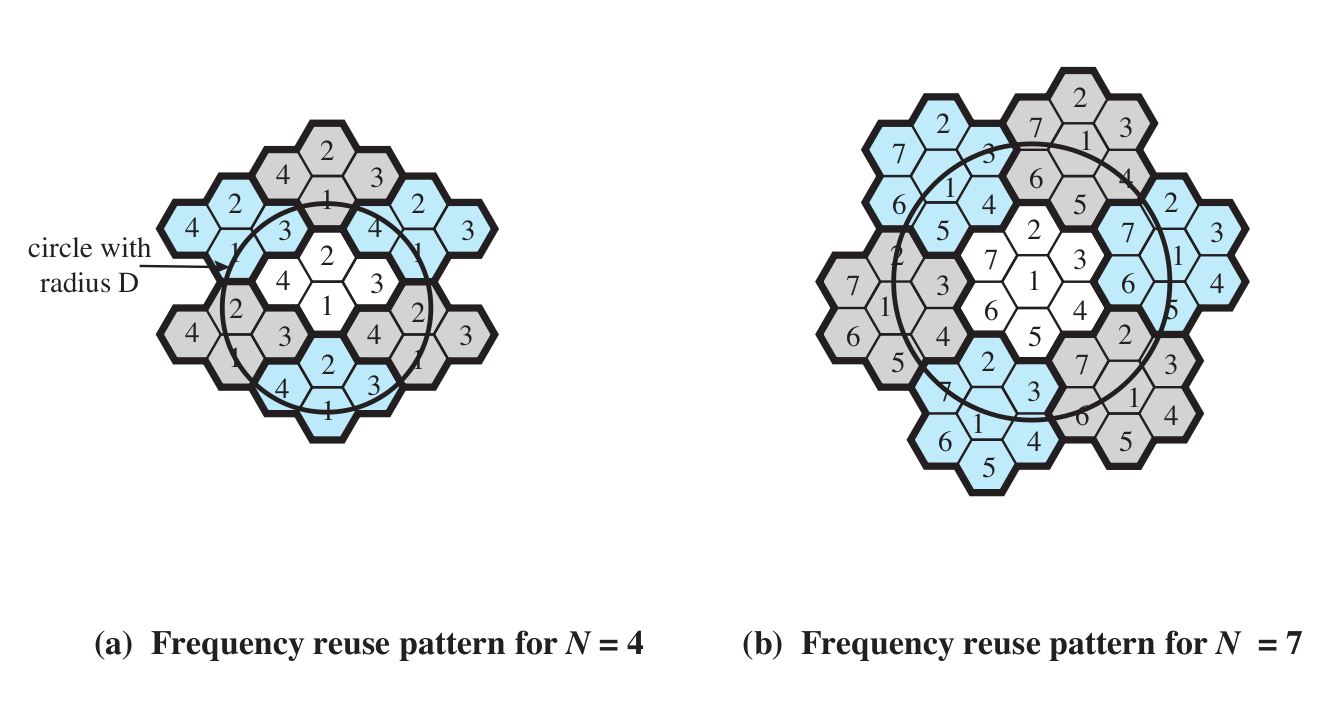
cell frequency-reuse patterns
As for cell reuse, TDMA requires that neighboring cells do not reuse the same frequencies. CDMA allows adjacent-cell frequency reuse. This is perhaps the biggest win for CDMA over TDMA; realistic gains are probably in the range of threefold.

Finally, CDMA may allow for more gradual signal degradation as the service is slightly "oversubscribed"; TDMA simply does not support that.

There is a deep relationship in CDMA between power and bandwidth, but in a good way: phones negotiate to use the smallest power for their needs

second reason for CDMA: allows gradual performance falloff with oversubscription

Chapter 14

Fig 14.1 on cell geometries: a cell diameter is typically a few miles, though in cities it can be much less
We already considered frequency-reuse patterns over cells, above; here are some other strategies for squeezing out more capacity
Fig 14.6 on finding phones: note that paging is pretty rare; phones instead "check in" regularly.


Fast (half-wavelength, or 6") fading v slow fading. Here's a diagram from the IEEE 802.11 wi-fi specification, illustrating the power-level fluctuations within a room. The wavelength here is about 5 inches, corresponding to the usual spacing between peaks.


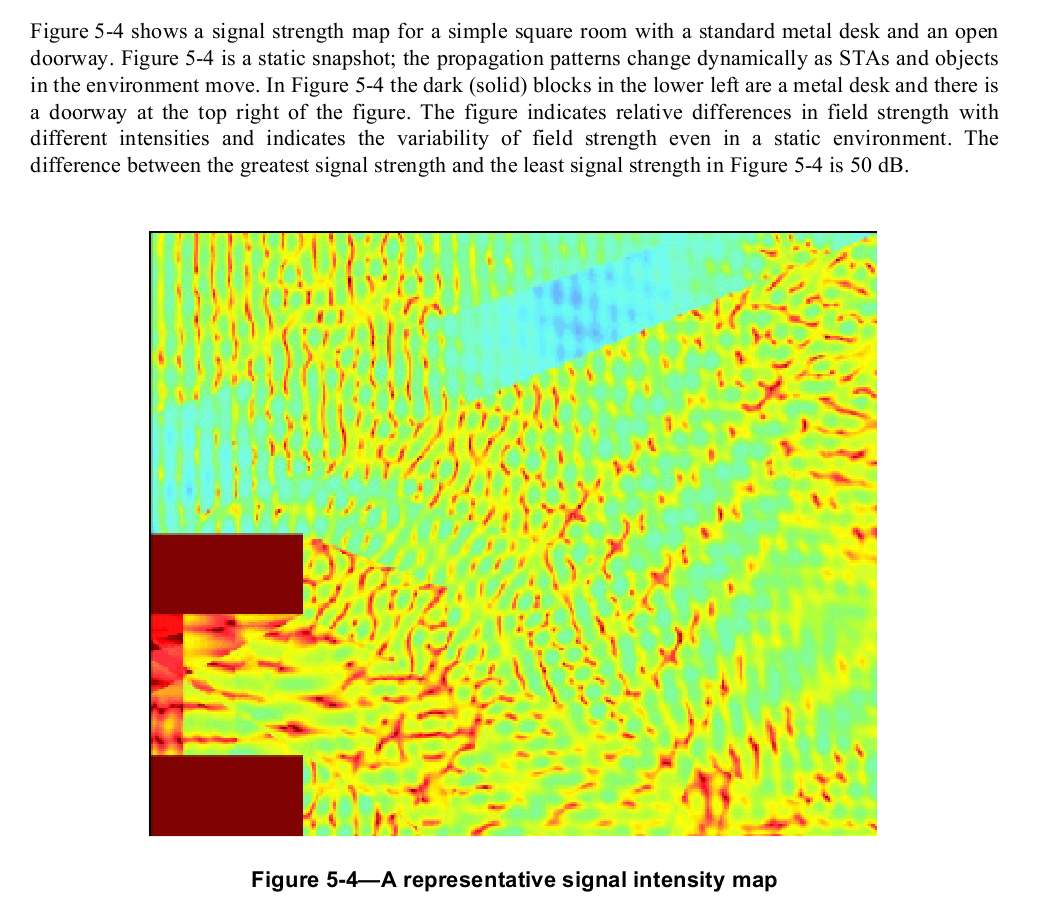
Fast Fading

AMPS: FDMA, analog
channel spacing 30kHz!!! This is so big because of multipath distortion (interference)

Multipath distortion:
Stallings Figure 14.7. Note there is no direct path in this figure! Normally, the reflected path is the worst offender, when compared with the direct path.
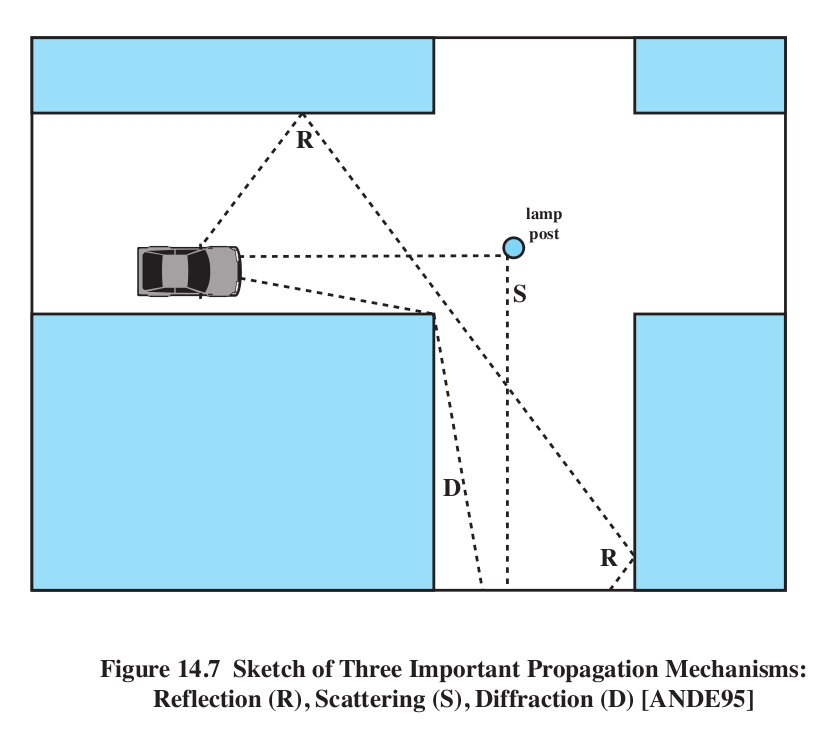
multipath interference

Phase distortion: multipath can lead to different copies arriving sometimes in phase and sometimes out of phase (this is the basic cause of "fast fading").

Intersymbol interference (ISI) and Fig 14.8. Pulses might be sent 1 unit apart, but multipath distortion might create "echo" pulses at times, say, 0.3, 0.5 and 0.9 units following the original pulse. That last echo is likely to interfere with the next data pulse.

Note that CDMA requires good power control by the phones so that all signals are roughly equal when received at the cell tower. Phones all adjust signal strength downwards if received base signal is stronger than the minimum.

Go through Andrews presentation at http://users.ece.utexas.edu/~jandrews/publications/cdma_talk.pdf
SMS (text messaging)
This originated as a GSM protocol, but is now universally available under CDMA as well, and these can be transmitted within SS7. Basically, the message piggybacks on "system" packets.

Walsh Codes

How are we going to get orthogonal codes? I tried (using brute-force search) to find a third code orthogonal to the length-6 A&C above or to A&B; there are none!

If k is a power of 2, we can do this with Walsh codes. We will create a k×k matrix of +1 and -1 where all the rows are orthogonal. This is done recursively.

k=1: the matrix is just [+]

k=2: the matrix is

+
 +
+
 −

k=4:

+
 +
 +
 +
+
 −
 +
 −
+
 +
 −
 −
+
 −
 −
 +

k=2r. Let M be the Walsh matrix of size 2r-1. Arrange four copies of M in a 2r × 2r matrix as follows, where −M is the result of flipping every entry in M:

M
 M
M
 −M

Note that this is what we did to go from k=1 to k=2 above, and from k=2 to k=4.

Erlang model

Suppose we know the average number of simultaneous users at the peak busy time (could be calls using a trunk line, could be calls to help desk). We would probably figure that at least some of the time, the demand might be higher than average. How many lines do we actually need?

To put this another way, suppose we flip 200 coins. The average number of heads is 100. What are the odds that in fact we get less than or equal to 110 heads? Or, to put it in a slightly more parallel way, suppose we keep doing this. We want to reward every head-getter, 99% of the time. How many rewards do we have to keep on hand?

One parameter is the acceptable blocking rate: the fraction of calls that are allowed to go unconnected (ie that receive the fast-busy or "reorder" signal). As this rate gets smaller, the number of lines needed will increase.

Example: how many lines do we need to handle a peak rate of 100 calls at any one time (eg 2,000 users each spending 5% of the day on the phone), and a maximum blocking rate of 0.01%?

(From http://erlang.com/calculator/erlb and my own program)

We assume that calls for which a line is not available are BLOCKED, not queued. (There is an alternative Erlang formulation for the queued model.) Here is a table; the call rate is the average number of simultaneous calls, and allowed blocking is the fraction of calls that can be blocked.


call rate
 allowed blocking
 lines needed
 excess
10
 0.01
 18
 180%
20
 0.01
 30
 150%
50
 0.01
 64
 128%
100
 0.01
 118
 118%
180
 0.01
 201
 111%
200
 0.01
 221
 110%
500
 0.01
 526
 105%
1000
 0.01
 1029
 103%

To a reasonable approximation, if we have 200 lines, we can handle ~180 calls.

Here's a table where the blocking rate is 0.001:

call rate
 allowed blocking
 lines needed
 excess
10  
0.001 21 210%
20
 0.001 35 175%
50
 0.001 71 142%
100
 0.001 128 128%
180
 0.001 216 120%
200
 0.001 237 119%
500
 0.001 554 111%
1000
 0.001 1071 107%


 The number of lines needed is always greater than the average peak rate. The question is by how much.

As allowed blocking rate goes down, the number of lines needed goes up, for the same call rate.

Also, as the call rate goes up, the number of extra lines goes up but the percentage of extra lines needed goes DOWN, due to the "law of large numbers"

            

ATM: Asynchronous Transfer Mode

versus STM: what does the "A" really mean?

Basic idea: virtual-circuit networking using small (53-byte) fixed-size cells

Review Fig 10.11 on large packets v small, and latency. (Both sizes give equal throughput, given an appropriate window size.)

basic cellular issues
delay issues:
Supposedly (see Peterson & Davie, wikipedia.org/wiki/Asynchronous_Transfer_Mode) smaller countries wanted 32-byte ATM because the echo would be low enough that echo cancellation was not needed. Larger countries wanted 64-byte ATM, for greater throughput. 48 was the compromise. (Search the WikiPedia article for "France".)

150 ms delay: threshhold for "turnaround delay" to be serious

packetization: 64kbps PCM rate, 8-16kbps compressed rate. Fill times: 6 ms, 24-48 ms respectively

buffering delay: keep buffer size >= 3-4 standard deviations, so buffer underrun will almost never occur. This places a direct relationship between buffering and jitter.

encoding delay: time to do sender-side compression; this can be significant but usually is not.

voice trunking (using ATM links as trunks) versus voice switching (setting up ATM connections between customers)

voice switching requires support for signaling

ATM levels:

A few words about how TCP congestion control works


ATM
basic argument (mid-1980s): Virtual circuit approach is best when different applications have very different quality-of-service demands (eg voice versus data)

why cells:

no-reordering rule, and its consequences