Normalization

Read in Elmasri & Navathe


Normalization refers to a mathematical process for decomposing tables into component tables; it is part of a broader area of database design. The criteria that guide this are functional dependencies, which should really be seen as user- and DBA-supplied constraints on the data.

Our first design point will be to make sure that relation and entity attributes have clear semantics. That is, we can easily explain attributes, and they are all related. E&N spells this out as follows:

E&N Guideline 1: Design a relation schema so that it is easy to explain its meaning. Do not combine attributes from multiple entity types and relationship types into a single relation.

As examples, consider
   
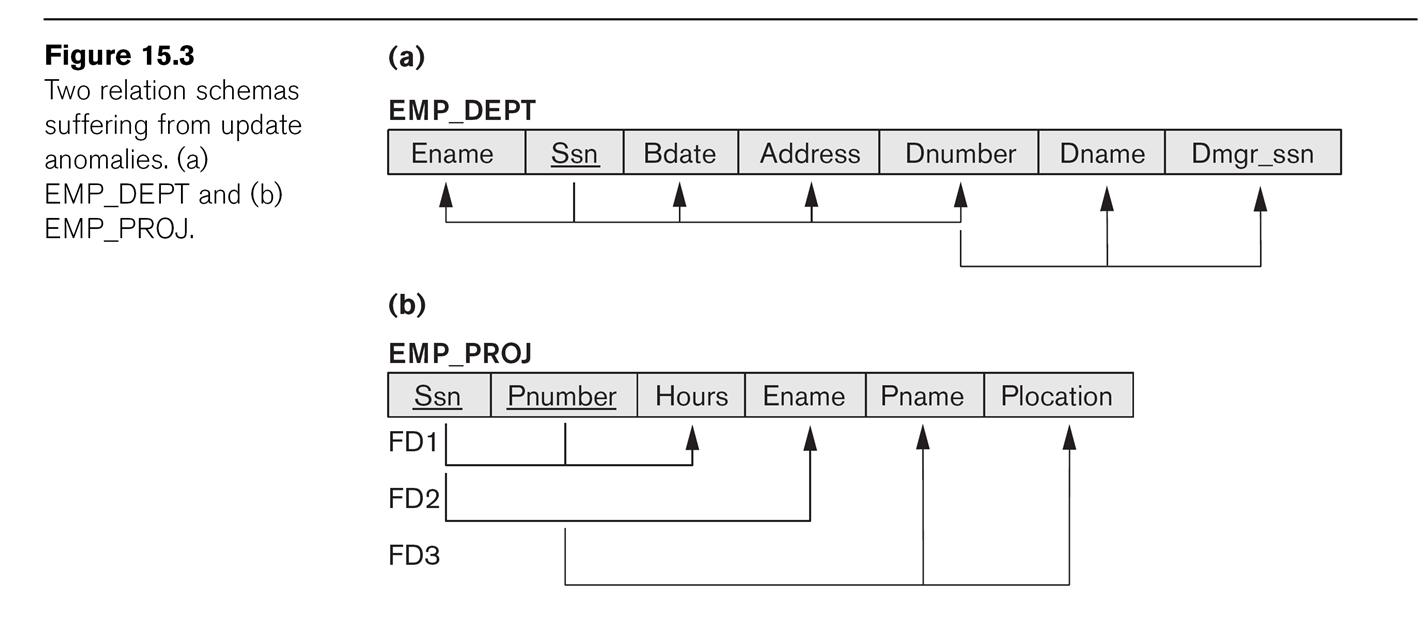
EMP_DEPT
    Ename
    Ssn
    Bdate
    Address
    Dnumber
    Dname
    Dmgr_ssn

create view emp_dept as select e.lname, e.ssn, e.bdate, d.dnumber, d.dname, d.mgr_ssn
from employee e join department d on e.dno = d.dnumber;

This mixes employee information with department information.

Another example is

EMP_PROJ
    Ssn
    Pnumber
    Hours
    Ename
    Pname
    Plocation

create view emp_proj as select e.ssn, p.pnumber, w.hours, e.lname, p.pname, p.plocation
from employee e, works_on w, project p where e.ssn=w.essn and w.pno = p.pnumber;

Both these later records can lead to anomalies of the following types:
This leads to

E&N Guideline 2: design your database so there are no insertion, deletion, or update anomalies. If this is not possible, document any anomalies clearly so that the update software can take them into account.

The third guideline is about reducing NULLs, at least for frequently used data. Consider the example of a disjoint set of inherited entity types, implemented as a single fat entity table. Secretaries, Engineers, and Managers each have their own attributes; every record has NULLs for two out of these three.

E&N Guideline 3: NULLs should be used only for exceptional conditions. If there are many NULLs in a column, consider a separate table.

The fourth guideline is about joins that give back spurious tuples. Consider

EMP_LOCS
    Ename
    Plocation

EMP_PROJ1
    Ssn
    Pnumber
    Hours
    Pname
    Plocation

If we join these two tables on field Plocation, we do not get what we want! (We would if we made EMP_LOCS have Ssn instead of Ename, and then joined the two on the Ssn column.) We can create each of these as a view:

create view emp_locs as select e.lname, p.plocation from employee e, works_on w, project p
where e.ssn=w.essn and w.pno=p.pnumber;

create view emp_proj1 as select e.ssn, p.pnumber, w.hours, p.pname, p.plocation
from employee e, works_on w, project p where e.ssn=w.essn and w.pno = p.pnumber;

Now let us join these on plocation:

select * from emp_locs el,  emp_proj1 ep where el.plocation = ep.plocation;

Oops. What is wrong?

E&N Guideline 4: Design relational schemas so that they can be joined with equality conditions on attributes that are appropriatedly related ⟨primary key, foreign key⟩ pairs in a way that guarantees that no spurious tuples are generated. Avoid relations that contain matching attributes that are not ⟨foreign key, primary key⟩ combinations.



Problem: what do we have to do to meet the above guidelines?

Functional Dependencies and Normalization

A functional dependency is a kind of semantic constraint. If X and Y are sets of attributes (column names) in a relation, a functional dependency X⟶Y means that if two records have equal values for X attributes, then they also have equal values for Y.

For example, if X is a set including the key attributes, then X⟶{all attributes}.

Like key constraints, FD constraints are not based on specific sets of records. For example, in the US, we have {zipcode}⟶{city}, but we no longer have {zipcode}⟶{areacode}.

In the earlier EMP_DEPT we had FDs
    Ssn ⟶  Ename, Bdate, Address, Dnumber
    Dnumber ⟶ Dname, Dmgr_ssn

In EMP_PROJ, we had FDs
    Ssn ⟶ Ename
    Pnumber ⟶ Pname, Plocation
    {Ssn, Pnumber} ⟶ Hours
 
Sometimes FDs are a problem, and we might think that just discreetly removing them would be the best solution. But they often represent important business rules; we can't really do that either. At the very least, if we don't "normalize away" a dependency we run the risk that data can be entered so as to make the dependency fail.

diagram for EMP_PROJ, EMP_DEPT


A superkey (or key superset) of a relation schema is a set of attributes S so that no two tuples of the relationship can have the same values on S. A key is thus a minimal superkey: it is a superkey with no extraneous attributes that can be removed. For example, {Ssn, Dno} is a superkey for EMPLOYEE, but Dno doesn't matter (and in fact contains no information relating to any other employee attributes); the key is {Ssn}.

Note that, as with FDs, superkeys are related to the sematics of the relationships, not to particular data in the tables.

Relations can have multiple keys, in which case each is called a candidate key. For example, in table DEPARTMENT, both {dnumber} and {dname} are candidate keys. For arbitrary performance-related reasons we designated one of these the primary key; other candidate keys are known as secondary keys. (Most RDBMSs create an index for the primary key, but not for other candidate keys unless requested.)

A prime attribute is an attribute (ie column name) that belongs to some candidate key. A nonprime attribute is not part of any key. For DEPARTMENT, the prime attributes are dname and dnumber; the nonprime are mgr_ssn and mgr_start.

A dependency X⟶A is full if the dependency fails for every proper subset X' of X; the dependency is partial if not, ie if there is a proper subset X' of X such that X'⟶A. If A is the set of all attributes, then the X⟶A dependency is full if X is a key, and is partial if X is a non-minimal superkey.


Normal Forms and Normalization

Normal Forms are rules for well-behaved relations. Normalization is the process of converting poorly behaved relations to better behaved ones.

First Normal Form

First Normal Form (1NF) means that a relation has no composite attributes or multivalued attributes. Note that dealing with the multi-valued location attribute of DEPARTMENT meant that we had to create a new table LOCATIONS. Composite attributes were handled by making each of their components a separate attribute.

Alternative ways for dealing with the multivalued location attribute would be making ⟨dnumber, location⟩ the primary key, or supplying a fixed number of location columns loc1, loc2, loc3, loc4. For the latter approach, we must know in advance how many locations we will need; this method also introduces NULL values.

Second Normal Form

Second Normal Form (2NF) means that, if K represents the set of attributes making up the primary key, every nonprime attribute A (that is an attribute not a member of any key) is functionally dependent on K (ie K⟶A), but that this fails for any proper subset of K (no proper subset of K functionally determines A).

Note that if a relation has a single-attribute primary key, as does EMP_DEPT, then 2NF is automatic. (Actually, the general definition of 2NF requires this for every candidate key; a relation with a single-attribute primary key but with some multiple-attribute other key would still have to be checked for 2NF.)

We say that X⟶Y is a full functional dependency if for every proper subset X' of X, X' does not functionally determine Y. Thus, 2NF means that for every nonprime attribute A, the dependency K⟶A is full: no nonprime attribute depends on less than the full key.

In the earlier EMP_PROJ relationship, the primary key K is {Ssn, Pnumber}. 2NF fails because {Ssn}⟶Ename, and {Pnumber}⟶Pname, {Pnumber}⟶Plocation.

Table Factoring

Given a relation ⟨K1, K2, A1, A2⟩ and a functional dependency, eg K1⟶A1, we can factor out the dependency into its own relationship and a reduced version of the original relationship. The original table has the righthand side of the dependency removed, and the new table consists of both sides of the dependency. In this case, we get:

original: ⟨K1, K2, A2⟩         -- A1 removed
new:       ⟨K1, A1⟩               -- both sides of K1⟶A1

To put a table in 2NF, use factoring. If two new tables have a common full dependency (key) on some subset K' of K, combine them. For EMP_PROJ, the result of factoring is:

    ⟨Ssn, Pnumber, Hours⟩
    ⟨Ssn, Ename⟩
    ⟨Pnumber, Pname, Plocation⟩

Note that Hours is the only attribute with a full dependency on {Ssn,Pnumber}.

The table EMP_DEPT is in 2NF, as is any table with a single key attribute.

Note that we might have a table ⟨K1, K2, K3, A1, A2, A3⟩, with dependencies like these:
    {K1,K2,K3}⟶A1 is full
    {K1,K2}⟶A2 is full (neither K1 nor K2 alone determines A2)
    {K2,K3}⟶A2 is full
    {K1,K3}⟶A3 is full
    {K2,K3}⟶A3 is full

The decomposition could be this, if we factor on {K1,K2}⟶A2 and then {K1,K3}⟶A3:

    ⟨K1, K2, K3, A1⟩
    ⟨K1, K2, A2⟩
    ⟨K1, K3, A3⟩

or it could be this, if we first factor on {K2,K3}⟶A2 and then on {K2,K3}⟶A3.

    ⟨K1, K2, K3, A1⟩
    ⟨K2, K3, A2⟩
    ⟨K2, K3, A3⟩

The latter two can be coalesced into ⟨K2, K3, A2, A3⟩. However, there is no way of continuing the first factorization approach and the second to find some common final factorization. We do not have unique factorization!
   
Remember, dependency constraints can be arbitrary! Dependency constraints are often best thought of as "externally imposed rules"; they come out of the user-input-and-requirements phase of the DB process. Trying to pretend that there is not a dependency constraint is sometimes a bad idea.

Consider the LOTS example of Fig 15.12.
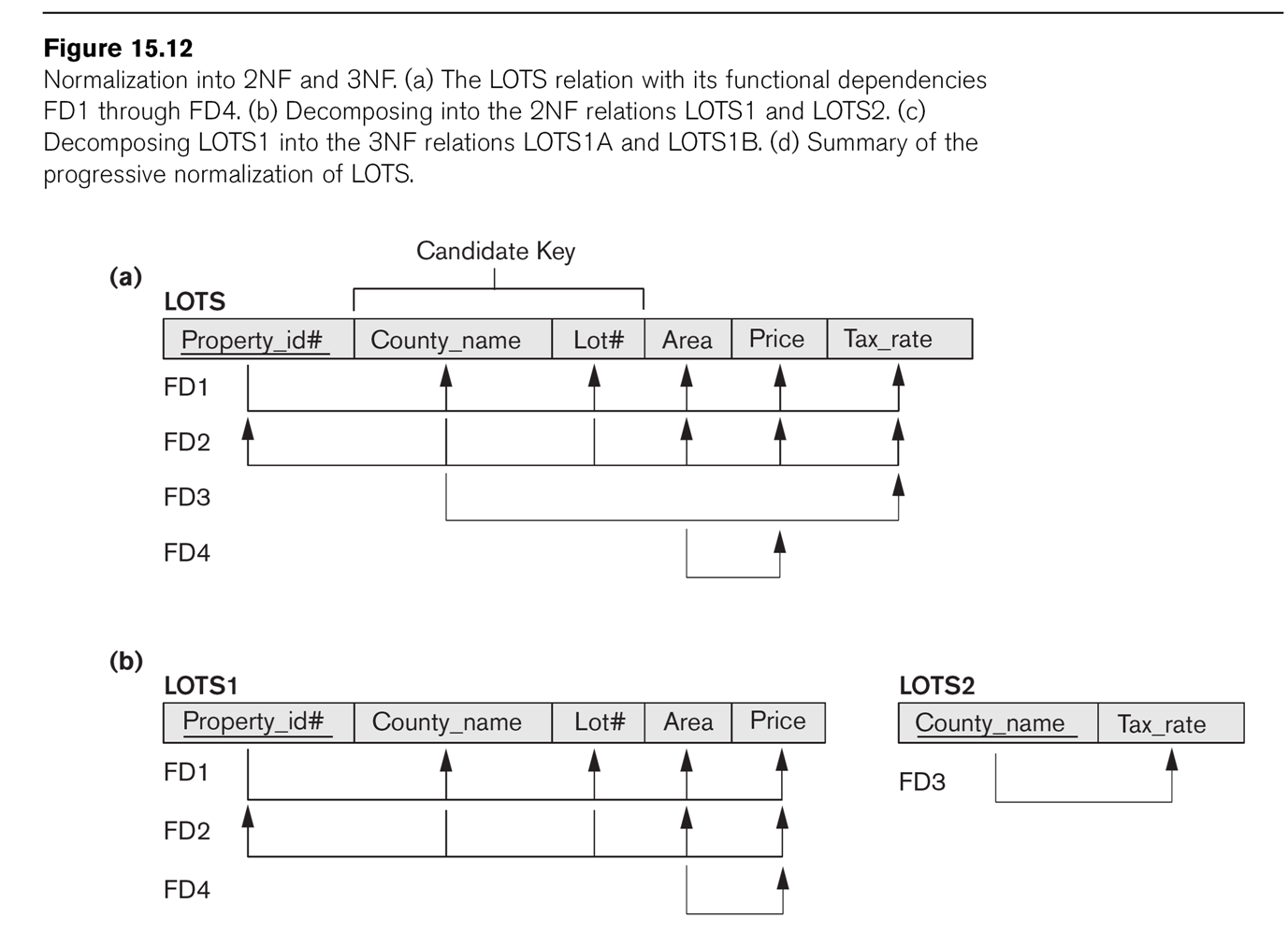
dependency diagram
Attributes for LOTS are
The primary key is property_ID, and ⟨county,lot_num⟩ is also a key. These are functional dependencies FD1 and FD2 respectively. We also have
    FD3: county ⟶ tax_rate
    FD4: area ⟶ price
(For farmland, FD4 is not completely unreasonable, at least if price refers to the price for tax purposes. In Illinois, the formula is tax_price = area × factor_determined_by_soil_type).

2NF fails because of the dependency county ⟶ tax_rate; FD4 does not violate 2NF. E&N suggest the decomposition into LOTS1(property_ID, county, lot_num, area, price) and LOTS2(county, tax_rate).

We can algorithmically use a 2NF-violating FD to define a decomposition into new tables. If X⟶A is the FD, we remove A from table R, and construct a new table with attributes those of X plus A. E&N did this above for FD3: county ⟶ tax_rate.

Before going further, perhaps two points should be made about decomposing too far. The first is that all the functional dependencies should still appear in the set of decomposed tables; the second is that reassembling the decomposed tables with the "obvious" join should give us back the original table, that is, the join should be lossless.

A lossless join means no information is lost, not that no records are lost; typically, if the join is not lossless then we get back all the original records and then some.

In Fig 15.5 there was a proposed decomposition into EMP_LOCS(ename, plocation) and EMP_PROJ1(ssn,pnumber,hours,pname,plocation). The join was not lossless.

Third Normal Form

Third Normal Form (3NF) means that the relation is in 2NF and also there is no dependency X⟶A for nonprime attribute A and for attribute set X that does not contain a candidate key (ie X is not a superkey). In other words, if X⟶A holds for some nonprime A, then X must be a superkey. (For comparison, 2NF says that if X⟶A for nonprime A, then X cannot be a proper subset of any key, but X can still overlap with a key or be disjoint from a key.)

2NF:  If K represents the set of attributes making up the primary key, every nonprime attribute A (that is an attribute not a member of any key) is functionally dependent on K (ie K⟶A), but that this fails for any proper subset of K (no proper subset of K functionally determines A).

3NF: 2NF + there is no dependency X⟶A for nonprime attribute A and for an attribute set X that does not contain a key (ie X is not a superkey).

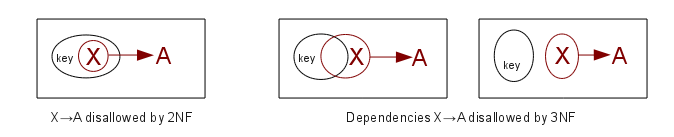
normal forms diagrams

Recall that a prime attribute is an attribute that belongs to some key. A nonprime attribute is not part of any key. The reason for the nonprime-attribute restriction on 3NF is that if we do have a dependency X⟶A, the general method for improving the situation is to "factor out" A into another table, as below. This is fine if A is a nonprime attribute, but if A is a prime attribute then we just demolished a key for the original table! Thus, dependencies X⟶A involving a nonprime A are easy to fix; those involving a prime A are harder.

If X is a proper subset of a key, then we've ruled out X⟶A for nonprime A in the 2NF step. If X is a superkey, then X⟶A is automatic for all A. The remaining case is where X may contain some (but not all) key attributes, and also some nonkey attributes. An example might be a relation with attributes K1, K2, A, and B, where K1,K2 is the key. If we have a dependency K1,A⟶B, then this violates 3NF. A dependency A⟶B would also violate 3NF.

3NF Table Factoring

Either case of a 3NF-violating dependency can be fixed by factoring out as with 2NF: if X⟶A is a functional dependency, then to factor out this dependency we remove column A from the original table, and create a new table ⟨X,A⟩. For example, if the ⟨K1, K2, A, B⟩ has 3NF-violating dependency K1,A⟶B, we create two new tables ⟨K1, K2, A⟩ and ⟨K1, A, B⟩. If the dependency were instead A⟶B, we would reduce the original table to ⟨K1, K2, A⟩ and create new table ⟨A,B⟩. Both the resultant tables are projections of the original; in the second case, we also have to remove duplicates.

Note again that if A were a prime attribute, then it would be part of a key, and factoring it out might break that key!

One question that comes up when we factor (for either 2NF or 3NF) is whether it satisfies the nonadditive join property (or lossless join property): if we join the two resultant tables on the "factor" column, are we guaranteed that we will recover the original table exactly? The answer is yes, provided the factoring was based on FDs as above. Consider the decomposition of R = ⟨K1, K2, A, B⟩ above on the dependency K1,A⟶B into R1 = ⟨K1, K2, A⟩ and R2 = ⟨K1, A, B⟩, and then we form the join R1⋈R2 on the columns K1,A. If ⟨k1,k2,a,b⟩ is a record in R, then ⟨k1,k2,b⟩ is in R1 and ⟨k1,a,b⟩ is in R2 and so ⟨k1,k2,a,b⟩ is in R1⋈R2; this is the easy direction and does not require any hypotheses about constraints.

The harder question is making sure R1⋈R2 does not contain added records. If ⟨k1,k2,a,b⟩ is in R1⋈R2, we know that it came from ⟨k1,k2,a⟩ in R1 and ⟨k1,a,b⟩ in R2. Each of these partial records came from the decomposition, so there must be b' so ⟨k1,k2,a,b'⟩ is in R, and there must be k2' so ⟨k1,k2',a,b⟩ is in R, but in the most general case we need not have b=b' or k2=k2'. Here we use the key constraint, though: if ⟨k1,k2,a,b⟩ is in R, and ⟨k1,k2,a,b'⟩ is in R, and k1,k2 is the key, then b=b'. Alternatively we could have used the dependency K1,A⟶B: if this dependency holds, then it implies that if R contains ⟨k1,k2,a,b⟩ and ⟨k1,k2,a,b'⟩, then b=b'.

This worked for either of two reasons: R1 contained the original key, and R2's new key was the lefthand side of a functional dependency that held in R.

In general, if we factor a relation R=⟨A,B,C⟩ into R1=⟨A,B⟩ and R2=⟨A,C⟩, by projection, then the join R1⋈R2 on column A might be much larger than the original R. As a simple example, consider Works_on = ⟨essn,pno,hours⟩; if we factor into ⟨essn,pno⟩ and ⟨pno,hours⟩ and then rejoin, then essn,pno will no longer even be a key. Using two records of the original data,

123456789
 1
 32.5
453453453
 1
 20

we see that the factored tables would contain ⟨123456789,1⟩ and ⟨1,20⟩, and so the join would contain ⟨123456789,1,20⟩ violating the key constraint.


The relationship EMP_DEPT of EN fig 15.11 is not 3NF, because of the dependency dnumber ⟶ dname (or dnumber ⟶ dmgr_ssn).
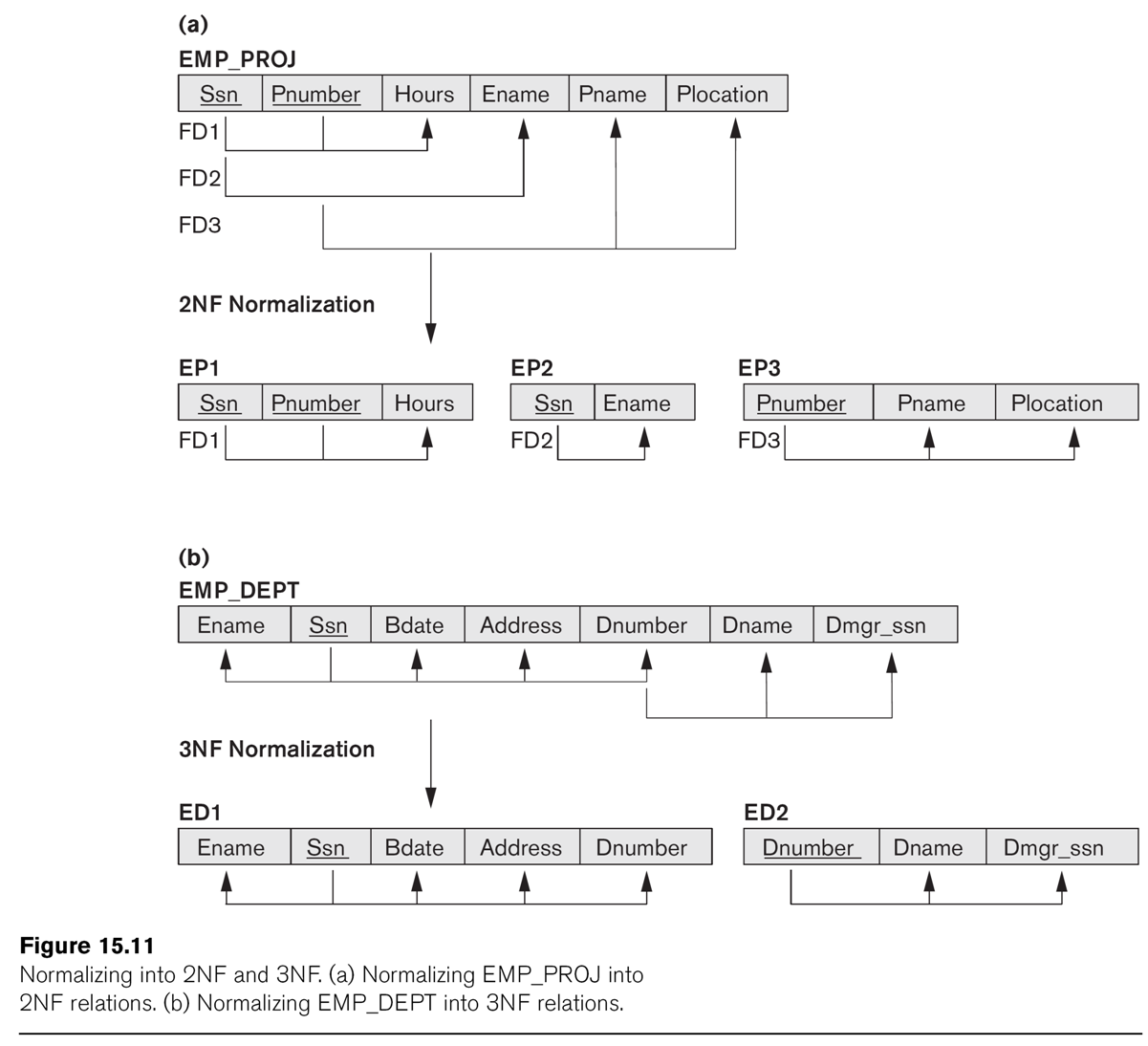
dependencies
Can we factor this out?

The LOTS1 relation above (EN fig 15.12) is not 3NF, because of Area ⟶ Price. So we factor on Area ⟶ Price, dividing into LOTS1A(property_ID, county,lot_num,area) and LOTS1B(area,price). Another approach would be to drop price entirely, if it is in fact proportional to area, and simply treat it as a computed attribute.

4343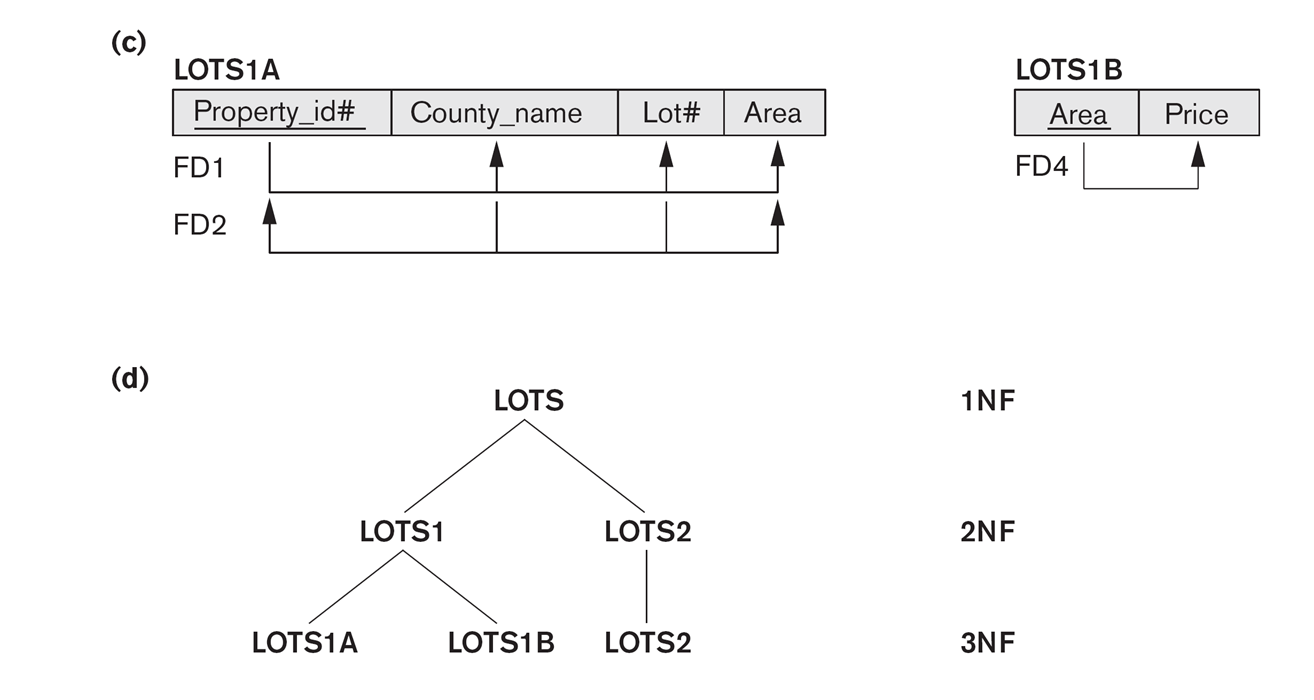

Multiple factoring outcomes

Consider a relation ⟨K1, K2, A, B, C⟩ where K1,K2 is the key and we have dependencies K1⟶B and B⟶C. If we try to put into 2NF first, by "factoring out" K1⟶B, we get tables ⟨K1,K2,A,C⟩ and ⟨K1,B⟩; the dependency B⟶C is no longer expressible in terms of the tables. But if we start by factoring out B⟶C, we get ⟨K1,K2,A,B⟩ and ⟨B,C⟩; we can now factor out K1⟶B which yields relations ⟨K1,K2,A⟩, ⟨K1,B⟩ and ⟨B,C⟩; all functional dependencies have now been transformed into key constraints. Factoring can lose dependencies, or, more accurately, make them no longer expressible except in terms of the re-joined tables.

An aid to dealing with this sort of situation is to notice that in effect we have a three-stage dependency: K1⟶B⟶C. These are often best addressed by starting with the downstream (B⟶C) dependency.

Boyce-Codd Normal Form

BCNF requires that whenever there is a nontrivial functional dependency X⟶A, then X is a superkey, even if A is a prime attribute. It differs from 3NF in that 3NF requires either that X be a superkey or that A be prime (a member of some key). To put it another way, BCNF bans all nontrivial nonsuperkey dependencies X⟶A; 3NF makes an exception if A is prime.

As for 3NF, we can use factoring to put a set of tables into BCNF. However, there is now a serious problem: by factoring out a prime attribute A, we can destroy an existing key constraint! To say this is undesirable is putting it mildly.

The canonical "formal" example of a relation in 3NF but not BCNF is ⟨A, B, C⟩ where we also have C⟶B. Factoring as above leads to ⟨A, C⟩ and ⟨C, B⟩. We have lost the key A,B! However, this isn't quite all it appears, because from C⟶B we can conclude A,C⟶B, and thus that A,C is also a key, and might be a better choice of key than A,B.

LOTS1A from above was 3NF and BCNF. But now let us suppose that DeKalb county lots have sizes <= 1.0 acres, while Fulton county lots have sizes >1.0 acres; this means we now have an additional dependency FD5: area⟶county. This violates BCNF, but not 3NF as county is a prime attribute. (The second author Shamkant Navathe is at Georgia Institute of Technology so we can assume DeKalb County is the one in Georgia, not the one in Illinois, and hence is pronounced "deKAB".)

If we fix LOTS1A as in Fig 15.13, dividing into LOTS1AX(property_ID,area,lot_num) and LOTS1AY(area,county), then we lose the functional dependency FD2: (county,lot_num)⟶property_ID.

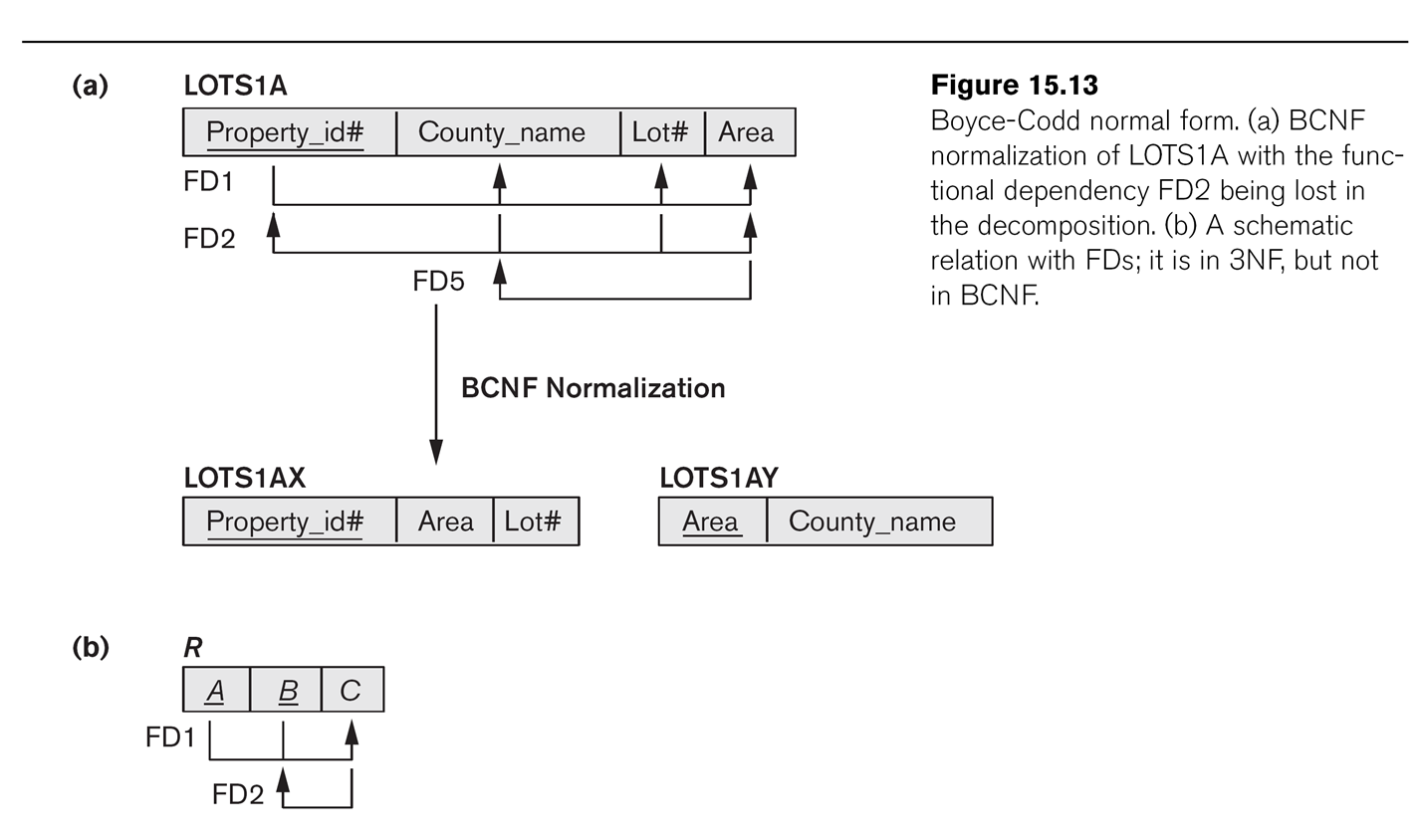
Where has it gone? This was more than just a random FD; it was a candidate key for LOTS1A.

All databases enforce primary-key constraints. One could use a CHECK statement to enforce the lost FD2 statement, but this is often a lost cause.

CHECK (not exists (select ay.county, ax.lot_num, ax.property_ID, ax2.property_ID
    from LOTS1AX ax, LOTS1AX ax2, LOTS1AY ay
    where ax.area = ay.area and ax2.area = ay.area       // join condition
    and ax.lot_num = ax2.lot_num
    and ax.property_ID <> ax2.property_ID))

We might be better off ignoring FD5 here, and just allowing for the possibility that area does not determine county, or determines it only "by accident".

Generally, it is good practice to normalize to 3NF, but it is often not possible to achieve BCNF. Sometimes, in fact, 3NF is too inefficient, and we re-consolidate for the sake of efficiency two tables factored apart in the 3NF process.


Fourth Normal Form

Suppose we have tables ⟨X,Y⟩ and ⟨X,Z⟩. If we join on X, we get ⟨X,Y,Z⟩. Now choose a particular value of x, say x0, and consider all tuples ⟨x0,y,z⟩. If we just look at the y,z part, we get a cross product Y0×Z0, where Y0={y in Y |  ⟨x0,y⟩ is in ⟨X,Y⟩} and Z0={z in Z |  ⟨x0,z⟩ is in ⟨X,Z⟩}. As an example, consider tables EMP_DEPENDENTS = ⟨ename,depname⟩ and EMP_PROJECTS = ⟨ename,projname⟩:

EMP_DEPENDENTS
ename
 depname
Smith
 John
Smith
 Anna


EMP_PROJECTS
ename
 projname
Smith
 projX
Smith
 projY

Joining gives
ename
 depname
 projname
Smith
 John
 X
Smith
 John
 Y
Smith
 Anna
 X
Smith
 Anna
 Y

Fourth normal form attempts to recognize this in reverse, and undo it. The point is that we have a table ⟨X,Y,Z⟩ (where X, Y, or Z may be a set of attributes), and it turns out to be possible to decompose it into ⟨X,Y⟩ and ⟨X,Z⟩ so the join is lossless. Furthermore, neither Y nor Z depend on X, as was the case with our 3NF/BCNF decompositions.

Specifically, for the "cross product phenomenon" above to occur, we need to know that if t1 = ⟨x,y1,z1⟩ and t2 = ⟨x,y2,z2⟩ are in ⟨X,Y,Z⟩, then so are t3 = ⟨x,y1,z2⟩ and t4 = ⟨x,y2,z1⟩. (Note that this is the same condition as in E&N, 15.6.1, p 533, but stated differently.)

If this is the case, then X is said to multidetermine Y (and Z). More to the point, it means that if we decompose into ⟨X,Y⟩ and ⟨X,Z⟩ then the join will be lossless.

Are you really supposed even to look for things like this? Probably not.

Fifth Normal Form

5NF is basically about noticing any other kind of lossless-join decomposition, and decomposing. But noticing such examples is not easy.


16.4 and the problems of NULLs

"There is no fully satisfactory relational design theory as yet that includes NULL values"

[When joining], "particular care must be devoted to watching for potential NULL values in foreign keys"

Unless you have a clear reason for doing otherwise, don't let foreign-key columns be NULL. Of course, we did just that in the EMPLOYEE table: we let dno be null to allow for employees not yet assigned to a department. An alternative would be to create a fictional department "unassigned", with department number 0. However, we then have to assign Department 0 a manager, and it has to be a real manager in the EMPLOYEE table.


Denormalization

Sometimes, after careful normalization to produce an independent set of tables, concerns about query performance lead to a regression to less-completely normalized tables, in a process called denormalization. This introduces the risk of inconsistent updates (like two records for the same customer, but with different addresses), but maybe that's a manageable risk. Maybe your front-end software can prevent this, and maybe it doesn't matter that much.

As an example, suppose we have the following tables, with key fields underlined. (Unlike the company database we are used to, projects here each have their own managers.)

project: pnumber, pname, mgr_ssn
employee: ssn, name, job_title, dno
works_on: essn, pid, hours

Now suppose management works mostly with the following view:

create view assign as
select e.ssn, p.pnumber, e.name, e.job_title, w.hours, p.pname, p.mgr_ssn, s.name
from employee e, project p, works_on w, employee s
where e.ssn = works_on.essn and works_on.pid = project.pnumber and p.mgr_ssn = s.ssn
That is a four-table join! Perhaps having a table assign would be more efficient.

Similarly, our earlier invoice table was structured like this:

invoice: invoicenum, cust_id, date
invitem: invoicenum, partnum, quantity, price
part: partnum, description, list_price
customer: cust_id, cust_name, cust_phone, cust_addr

To retrieve a particular customer's invoice, we have to search three tables. Suppose we adopt instead a "bigger" table for invoice:

invoice2: invoicenum, cust_id, cust_name, cust_phone, date, part1num, part1desc, part1quan,
    part2num, part2desc,part2quan, part3num, part3desc,part3quan, part4num, part4desc,part4quan

That is, invoice2 contains partial information about the customer, and also information about the first four items ordered. These items will also appear in invitem, along with any additional parts.

This means that most queries about the database can be displayed by examining only a single table. If this is a web interface, there might be a button users could click to "see full order", but the odds are it would seldom be clicked, especially if users discovered that response was slow.

The important thing for the software developers is to make sure that the invoice2 and invitem  and customer tables, which now contain a good deal of redundant information, do not contain any inconsistencies. That is, whenever the customer's information is updated, then the invoice2 table needs to be updated too. A query such as the following might help:

select i.invoicenum, i.cust_id, i.cust_name, c.cust_name, i.cust_phone, c.cust_phone
from invoice2 i join customer c on i.cust_id = c.cust_id
where i.cust_name <> c.cust_name or i.cust_phone <> c.cust_phone

We might even keep both invoice and invoice2, with the former regarded as definitive and the latter as faster.

The value invoice2.cust_phone might be regarded as redundant, but it also might be regarded as the phone current as of the time the order was placed. Similarly, the invitem.price value can be different from the part.list_price because invitem.price represents either the price as of the date the order was placed or else a discounted price.

Denormalization can be regarded as a form of materialized view; that is, the denormalized table actually exists somewhere, and is updated (or reconstructed) whenever its base tables are updated. However, if we create the denormalized table on our own, without a view, then we have more control over how often the table gets updated. Perhaps the management assign table above would only need to be updated once a day, for example.

Denormalization works best if all the original tables involved are too large to be stored in memory; the cost of a join with a table small enough to fit in memory is quite small. For this reason, the invoice2 example might be better than the assign example, for which the tables are mostly "small".

Facebook makes significant use of denormalization at times. One of their best-known examples is Timeline. See highscalability.com/blog/2012/1/23/facebook-timeline-brought-to-you-by-the-power-of-denormaliza.html, and the actual FB blog on which that article was based: https://www.facebook.com/note.php?note_id=10150468255628920.

The basic issue is that the individual posts on your Timeline may be scattered all over the place. In particular, many of the posts were originally associated with other users, and they have either been shared to your Timeline, or Facebook has decided to display them on your timeline too (Facebook's "Multifeed Aggregator" makes decisions here). While all of your direct posts (and replies) might be on the same disk partition, that's not likely for posts that started on someone else's Timeline, eg when Alice posts something to her page and also to Bob and Charlie's pages. Here's the summary of the problem:

Before we began Timeline, our existing data was highly normalized, which required many round trips to the databases. Because of this, we relied on caching to keep everything fast. When data wasn’t found in cache, it was unlikely to be clustered together on disk, which led to lots of potentially slow, random disk IO. To support our ranking model for Timeline, we would have had to keep the entire data set in cache, including low-value data that wasn’t displayed.

After denormalization, the data is sorted by (user, time). Copies of posts are made as necessary, so that most Timeline data for one user is on one disk (or disk cluster). Fetching records just by (user) is quite fast. When the same post is to be displayed on the timelines of two or more users; the denormalization here means that we make as many copies of the post as necessary. See also big_data.html#sharding.

Finally, this is an interesting blog post: kevin.burke.dev/kevin/red

[Reddit keeps] a Thing Table and a Data Table. Everything in Reddit is a Thing: users, links, comments, subreddits, awards, etc. Things keep common attributes like up/down votes, a type, and creation date. The Data table has three columns: thing id, key, value. There’s a row for every attribute. There’s a row for title, url, author, spam votes, etc. When they add new features they didn’t have to worry about the database anymore. They didn’t have to add new tables for new things or worry about upgrades. Easier for development, deployment, maintenance.

It works for them. YMMV.