Cellular Telephony
Peter Dordal, Loyola University CS Department
Cellular telephony involves mobile phones communicating with a base
station. The base station and its connected phones is called a cell.
Cells have approximate but not strict geographic boundaries; a phone near
the border can belong to the cell on either side.
When a mobile phone moves from one cell to another, it is transferred via a
handoff. This can apply whether a call is in progress or
not.
Cellular issues: neighboring cells interfere with each other!
Cellular phones must also resist eavesdropping (though encryption is the
"right" way to do that)
Cell phones must somehow deal with multipath distortion!!
Three modulation techniques:
- FDMA: Frequency Division Mulitple Access: essentially FM; everyone
talks on a different channel
- TDMA: Time Division Multiple Access: essentially time-division
multiplexing; everyone talks one at a time, quickly, during their own
time slot
- CDMA: Code Division Multiple Access: everyone talks in a different
language? Or listen to multiple people speaking simultaneously; it's
usually not too hard to follow one particular speaker.
CDMA handles multipath distortion (reflected, delayed copies of the original
signal) better than the others. While all three are theoretically equally
efficient in terms of signal bandwidth, in practice the latter two need
guard bands to handle multipath distortion, and so CDMA allows more
channels. CDMA allows reuse of frequencies from adjoining
cells, for a seven-fold improvement over TDMA/FDMA. It also may allow more
graceful signal degradation as the channel is oversubscribed.
Hedy Lamarr, b. 1914, Vienna
One of the great actresses of Hollywood's golden era: wikipedia.org/wiki/Hedy_Lamarr
Inventor of Frequency-Hopping Spread Spectrum
Spread Spectrum
9.2: FHSS & Hedy Lamarr /
George Antheil
Both parties generate the same PseudoNoise [PN] sequence. The carrier
frequency jumps around according to PN sequence.
In Lamarr's version, player-piano technology would have managed this; analog
data was used. Lamarr's intent was to avoid radio eavesdropping (during
WWII); an eavesdropper wouldn't be able to guess the PN sequence and thus
would only hear isolated snippets.
Here is a diagram illustrating basic MFSK (multiple frequency-shift keying),
in which we use 2L frequencies to transmit L bits at a time (see
Fig 5.9)
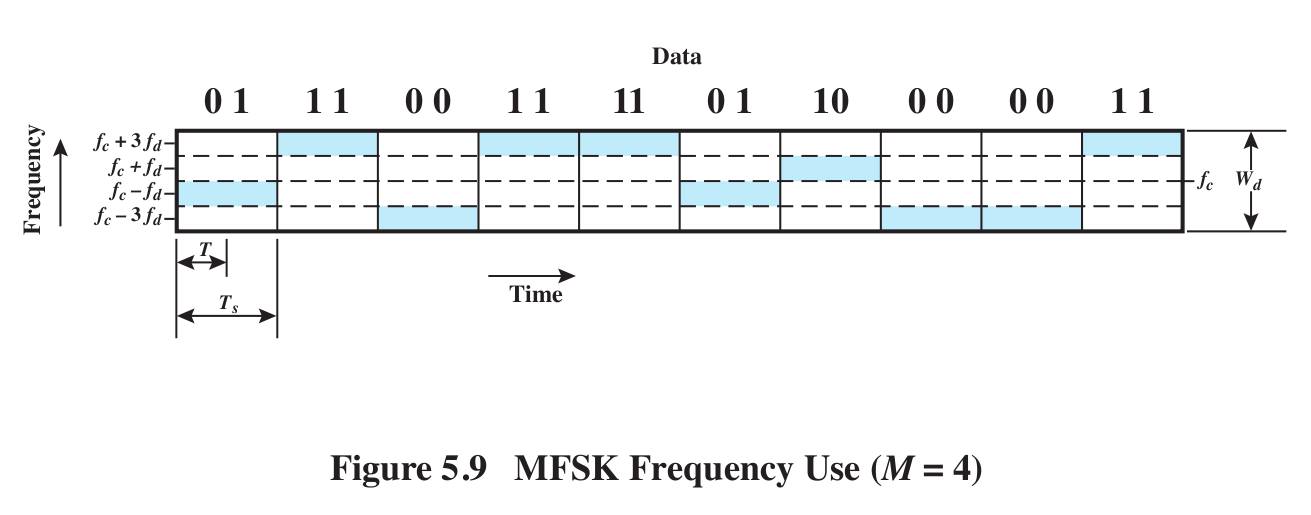
With Frequency-Hopping Spread Spectrum (FHSS) we duplicate
the above encoding on any of several frequency bands, each large enough to
contain all the frequencies above.
Here's a colorized version of Stallings fig 9.4. We will use a
"pseudo-noise" or pseudo-random (PN) sequence to spread the frequencies of
MFSK over multiple "blocks"; each MFSK instance uses one block. Each
endpoint can compute the PN sequence, but to the world in between it appears
random. For each distinct PN symbol we will use a band like the MFSK band
above, but we'll have multiple such bands all stacked together, a different
band for each distinct PN symbol.
- Tc: time for each unit in the PN sequence
- Ts: time to send one block of L bits
The PN sequence chooses the appropriate broad color band; the four possible
values of a data symbol choose one of the four sub-bands within a broad
colored band.
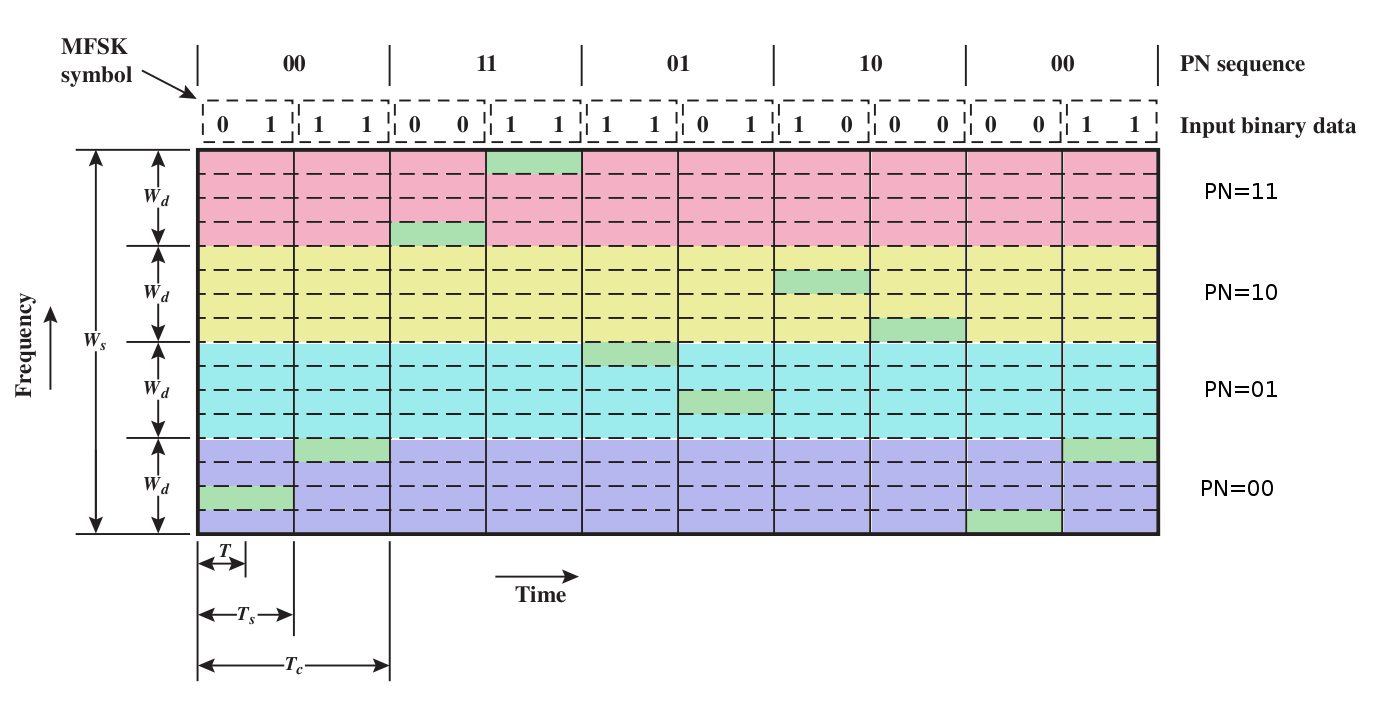
Note one individual frequency is used to encode L bits; we need 2L frequencies
in
all to send all L-bit patterns. We are also sending the data two bits at a
time, using the two bits to choose one of four frequencies. If we switched
to binary (one bit at a time, L=1), then we would only need two frequencies
(two of the narrow horizontal bands). But for the same data rate we'd only
have half as much time (Ts
/ 2) to identify each frequency, so each narrow band would have to be twice
as wide. Bottom line: we'd have the same bandwidth requirement.
MFSK does a simple form of frequency hopping already. The goal of FHSS/MFSK
is to greatly increase the hopping range
slow v fast FHSS/MFSK: Fig 9.4 (above) v Fig
9.5
slow: Tc >= Ts: send >= 1 block of bits for each
PN tick
fast: Tc < Ts: use >1 PN tick to send each block
of bits
feature of fast: we use two or more frequencies to transmit each symbol; if
there's interference on one frequency, we're still good.
Consider 1 symbol = 1 bit case
If we use three or more frequencies/symbol, we can resolve errors with
"voting"
What is this costing us?
9.3: Direct-Sequence Spread Spectrum
(DSSS)
Each bit in original becomes multiple bits, or chips.
We end up using a lot more bandwidth for the same amount of information! The
purpose: resistance to static and interference (especially multipath
interference).
Same spreading concept as fast FHSS, but stranger.
Basically we modulate the signal much "faster", which spreads the bandwidth
as a natural consequence of modulation. We no longer have a discrete set of
"channels" to use.
Suppose we want to use n-bit spreading. Each side, as before, has access to
the same PN sequence. To send a data bit, we do the following:
- get n bits from the PN sequence
- XOR the data bit with the entire n-bit sequence (that is, if the data
bit is 1, we invert)
- transmit those n bits
Note that we are transmitting n
bits in order to communicate one
bit. The receiver then:
- receives n bits
- XORs them with the next n bits of the PN sequence
- expects all 0's or else all 1's.
See Figure 9.6.
For every data bit, we will actually receive n bits. Those n bits, XORed
with the appropriate n bits from the PN sequence, should give either n
0-bits or n 1-bits. A few wrong bits won't matter; we can simply go with the
majority.
Recall that AM band-width was proportional to the band-width of the signal.
The same thing is happening here: if sending the data 1 bit at a time needed
a band-width of B, then sending n bits at a time will likely need a
band-width of about nB. Thus, like FHSS, we've greatly expanded the
band-width requirement.
Sometimes it is easier to think of the signal as taking on values +1 and -1,
rather than 0/1. Then, we can multiply
the data bit by the n-bit PN sequence; multiplication by -1 has the effect
of inverting.
Figure 9.9 shows the resultant
spectrum. Because we're sending at a n-times-faster signaling rate, our
spectrum is also n times wider. Why would we want that? Because jamming
noise is likely to be isolated to a small part of the frequency range; after
the decoding process, the jamming power is proportionally less.
9.4: CDMA
Here, each sending channel is assigned a k-bit chipping
code; each data bit becomes k "chips" (k is often ~128, though in
our examples we'll use k=4 or k=6); these replace the PN sequence (mostly;
see below). Each receiver has the corresponding chipping code. The chips are
sent using FHSS or DSSS; for DSSS, the sender sendsthe chipping code for a
0-bit and the inverted chipping code for a 1-bit.
As with FHSS and DSSS, one consequence is that data is spread out over a
range of frequencies, each with low power.
Unlike these, however, we are now going to allow multiple transmissions simultaneously, at least in the forward
(tower to cellphones) direction. The signals to each phone, each with a
unique chipping code, are added together and transmitted together; the
receivers need to pick their own data bit out of the chaos.
basic ideas:
chipping codes: These are the
sequences of k bits that we give each user, eg ⟨1,0,1,1,0,0⟩.
The algebra is more tractable if we instead treat 0 as -1, so the code above
would become ⟨1,-1,1,1,-1,-1⟩.
dot product: Given two sequences of
numbers A = ⟨a1,a2,a3,a4,a5⟩ and B = ⟨b1,b2,b3,b4,b5⟩, the dot product, or inner product, is
A∙B = a1×b1 + a2×b2 + a3×b3 + a4×b4 + a5×b5
If our sequences represent vectors in 3-dimensional space (that is, the
sequences have length 3), then A∙B=0 if and only if A and B are
perpendicular, or orthogonal.
Suppose we have some pairwise-orthogonal sequences, say A, B, C, and D, of
any dimension (length); that is, A∙B = B∙C = A∙C = A∙D = B∙D = C∙D = 0; any
two are perpendicular. Then, if we're given a vector E = a×A + b×B + c×C +
d×D (where a,b,c,d are ordinary real numbers; multiplying a vector by a real
number just means multiplying each component by that number: 2×⟨3,5,7⟩ =
⟨6,10,14⟩), we can immediately solve for a,b,c,d, regardless of our
geometrical interpretation:
E = a×A + b×B + c×C + d×D
E∙A = a×A∙A + b×B∙A + c×C∙A + d×D∙A
=
a×A∙A (because B∙A = C∙A = D∙A = 0)
and so a = E∙A / A∙A. Similarly we can recover b, c and d. Usually we'll
scale each of the A,B,C,D so A∙A = 1, so a = A∙E. (We don't do this below,
so A∙A = 6.)
The simplest set of orthogonal vectors, or chipping codes, is
⟨1,0,0,0,0,0⟩, ⟨0,1,0,0,0,0⟩, ⟨0,0,1,0,0,0⟩, etc. But it's not the only set,
as we'll see below.
Suppose we have K users wanting to transmit using CDMA. Each user will be
given a vector of 0's and 1's (or -1's and 1's, depending on our
perspective) of length k; this is the user's chipping code. Each user
transmits k "chips" on k frequencies at the same time. Ideally we use K=k,
but in practice K can be rather larger. All the transmissions add together,
linearly (actually, we'll have to adjust the individual cellphone power
levels so that, at the base antenna, all the signals have about the same
power). The transmissions are done in such a way that the receiver can
extract each individual signal, even though all the signals overlap.
Similarly, when the base station wants to transmit to all K users, combines
all K bits for each of k positions and transmits the whole mess; each
individual receiver can extract its own signal.
Trivial way to do this: ith sender sends on frequency i only, and does
nothing on other frequencies. This is just FDM, corresponding to the
chipping codes ⟨1,0,0,0,0,0⟩, ⟨0,1,0,0,0,0⟩, ⟨0,0,1,0,0,0⟩, etc. We don't
want to use this, though.
Example from Table 9.1:
codeA
|
1
|
-1
|
-1
|
1
|
-1
|
1
|
codeB
|
1
|
1
|
-1
|
-1
|
1
|
1
|
codeC
|
1
|
1
|
-1
|
1
|
1
|
-1
|
codeA∙codeB = 0, codeA∙codeC = 0, codeB∙codeC = 2 (using ∙ for "dot
product")
userA sends (+1)×codeA or (-1)×codeA
suppose D = data = a×codeA + b×codeB, a,b = ±1
Then D∙codeA = a×codeA∙codeA + b×codeB∙codeA = a×6 + b×0 = 6a; we have
recovered A's bit!
Similarly D∙codeB = a×codeA∙codeB + b×codeB∙codeB = a×0 + b×6 = 6b, and we
have recovered B's bit!
Now suppose the transmission D = -1×codeA + 1×codeB + 1×codeC. Can we
recover the respective -1, 1 and 1?
combined data D
|
1
|
3
|
-1
|
-1
|
3
|
-1
|
|
codeA
|
1
|
-1
|
-1
|
1
|
-1
|
1
|
|
products w D
|
1
|
-3
|
1
|
-1
|
-3
|
-1
|
sum = -6
|
codeB
|
1
|
1
|
-1
|
-1
|
1
|
1
|
|
products w D
|
1
|
3
|
1
|
1
|
3
|
-1
|
sum = 8
|
codeC
|
1
|
1
|
-1
|
1
|
1
|
-1
|
|
products w D
|
1
|
3
|
1
|
-1
|
3
|
1
|
sum = 8
|
Algebraically, D∙codeA = -1×codeA∙codeA = -6, because codeA is orthogonal to
codeB and codeC
D∙codeB = -1×codeA∙codeB + 1×codeB∙codeB + 1×codeC∙codeB = -1×0 + 1×6 + 1×2
= 8. codeB and codeC are not orthogonal but they are "close"; codeB∙codeC is
"small" relative to 6.
Similarly, D∙codeC = -1×codeA∙codeC + 1×codeB∙codeC + 1×codeC∙codeC = -1×0 +
1×2 + 1×6 = 8.
Whenever codeB and codeC appear in the mix, we'll have an extra ±2 in the
mix. But the expected answer is -6, 0, or 6, so if we round to the nearest
such value we'll get the correct result.
Cell phones
analog
The AMPS standard used FDMA (Freq Division Multiple Access): allocates a
30kHz channel to each call (2 channels!), held for duration of call.
TDMA
digitizes voice, compresses it 3x, and then uses TDM to send 3 calls over
one 30kHz channel.
GSM
form of TDMA with smaller cells, more dynamic allocation of cells. Note that
if everyone talks at once, there might not be enough cells for all!
Data form: GPRS (General Packet Radio Service)
CDMA
sprint PCS, US Cellular, others
code division multiple access: kind of weird. This is a form of "spread
spectrum". Signals are encoded, and spread throughout the band. Any one bit
is sent as ~128 "chips", but chips may be used by multiple senders.
Demultiplexing is achieved because codes are "orthogonal", as above.
This strategy may give good gradual degradation as the number of calls
increases (assuming suitable chipping codes can be found), and good
eavesdropping prevention (though not as good as strong encryption). It also
gives excellent bandwidth utilization.
Note that we can only use this orthogonal-chipping-code strategy in the forward direction (tower to cellphones);
for orthogonal codes to work, all the transmissions must be precisely
synchronized. In the reverse
direction, we might have had all the cellphones obey some synchronization
protocol, but we don't; instead of orthogonal codes we use pseudorandom
sequences. Given two random sequences A and B, of length N, the
inner product A∙B is typically 0.8×sqrt(N) (unless A=B, in which case A∙B =
N). We can't have N cellphones transmit simultaneously and expect the
antenna to decode, but we can have sqrt(N), and furthermore the phones do
not have to be synchronized in any way.
There is some debate about exactly why CDMA works better than TDMA;
theoretically, bandwidth use should be the same. However, the big wins for
CDMA appear to be in avoiding multipath distortion and in frequency
reuse in neighboring cells. If one or two frequencies are affected
by multipath (which is usually very frequency-dependent), the other
frequencies over which CDMA spreads the signal can take up the slack.
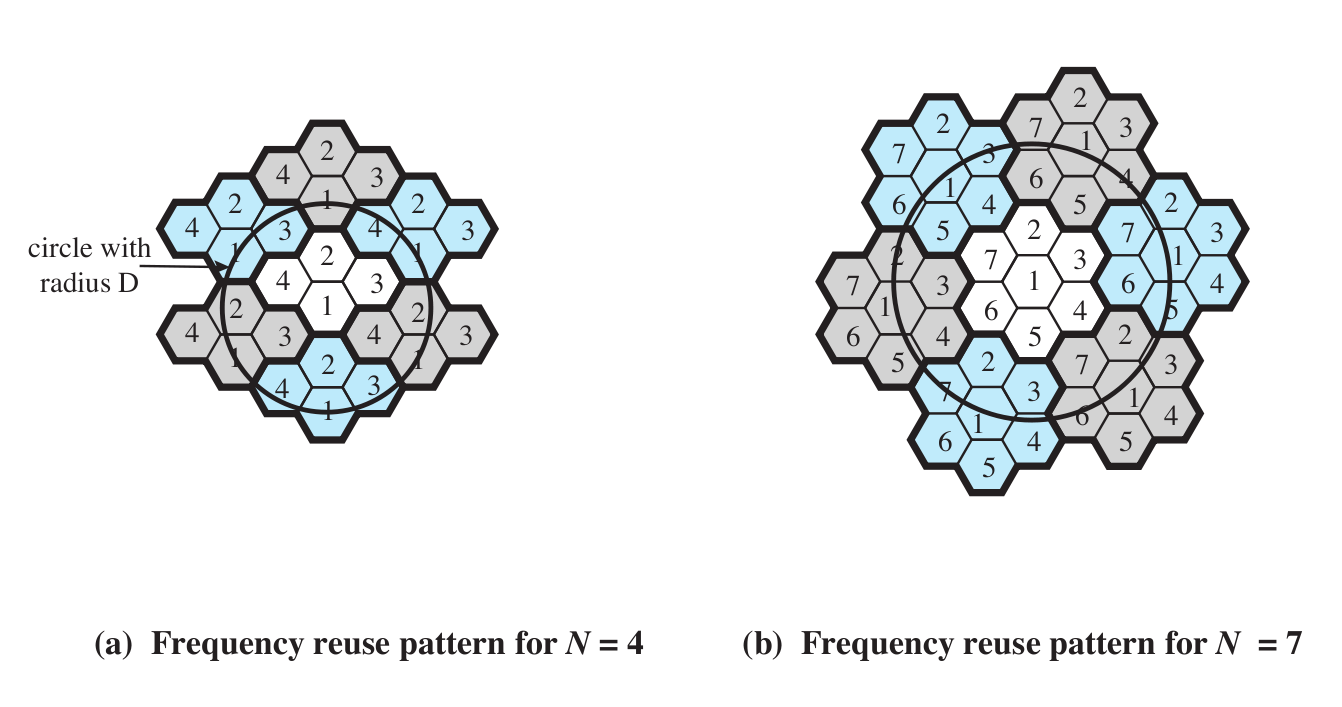
Here is Stallings figure 14.2 (at least the N=4 and N=7 cases; the book also
illustrates a N=19 example).
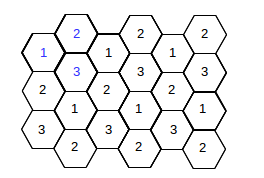
We can also do this for N=3:
As for cell reuse, TDMA requires that neighboring cells do not reuse the
same frequencies. CDMA allows adjacent-cell frequency reuse. This is perhaps
the biggest win for CDMA over TDMA; realistic gains are probably in the
range of threefold.
Finally, CDMA may allow for more
gradual signal degradation as the service is slightly "oversubscribed"; TDMA
simply does not support that.
There is a deep relationship in CDMA between power and bandwidth, but in a
good way: phones negotiate to use the smallest power for their needs
second reason for CDMA: allows gradual performance falloff with
oversubscription
Cell sizes
A full-sized cell diameter is typically a few miles, though in cities it can
be much less.
We already considered frequency-reuse patterns over cells, above; here are
some other strategies for squeezing out more capacity
- cell sectoring
- cell splitting (works down to ~ 100 m; cells smaller than ~1km are
known as microcells)
- adding frequencies ($$$)
- frequency borrowing
- microcells
Phones can stay in touch with towers either by having the phone check in or
having the tower page the phone. The latter is pretty rare; phones instead
"check in" regularly.
A microcell is a cell transmitter (a "tower") that might
cover one building, or part of an airport.
A picocell is even smaller: one airplane, one floor, or
something like that.
A femtocell is sort of the cellular equvalent of Wi-Fi.
You can get one for your house (for a little over $100), but be aware that
you may have to have your cellular provider's cooperation to get your phone
to "trust" the femtocell. Alternatively, the femtocell can be configured to
accept only certain numbers. Someone in control of the femtocell can easily
eavesdrop on all calls through it.
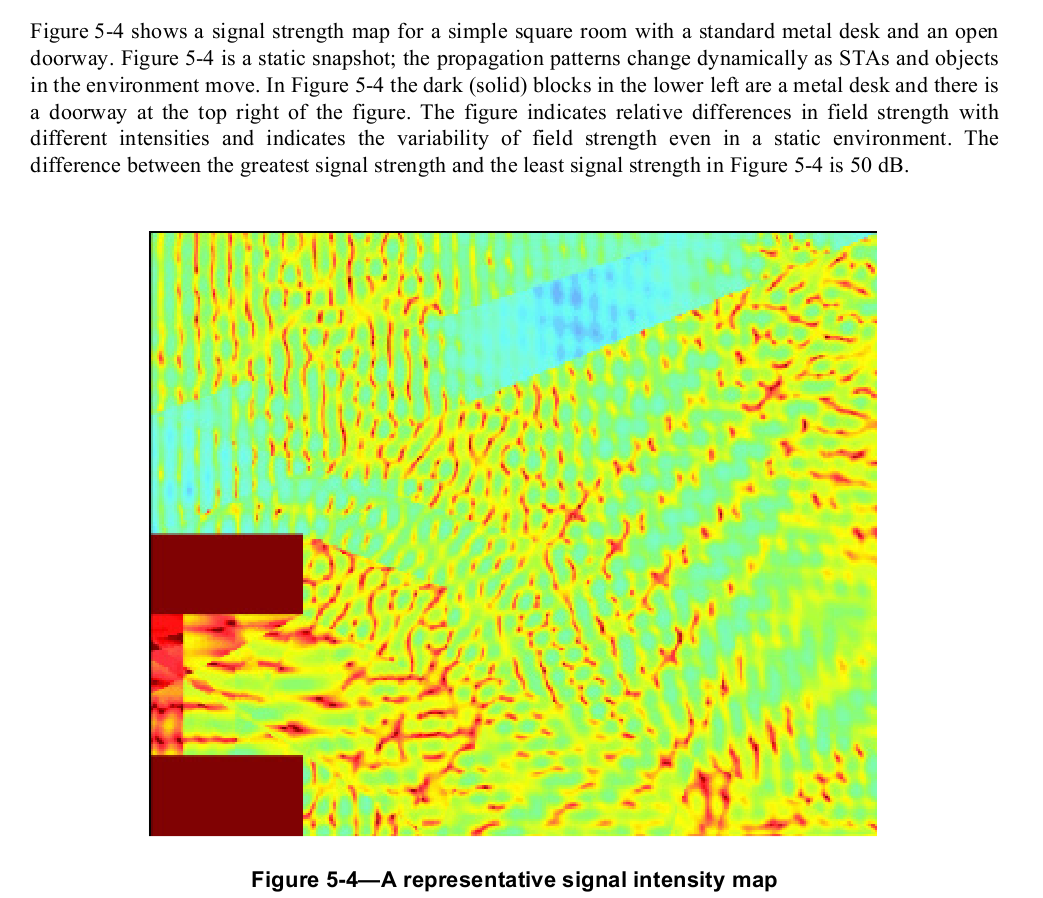
Fading
Fast (half-wavelength, or 6") fading v slow fading. Here's a diagram from
the IEEE 802.11 wi-fi specification, illustrating the power-level
fluctuations within a room. The wavelength here is about 5 inches,
corresponding to the usual spacing between peaks.
AMPS: FDMA, analog
channel spacing 30kHz!!! This is so big because of multipath distortion
(interference)
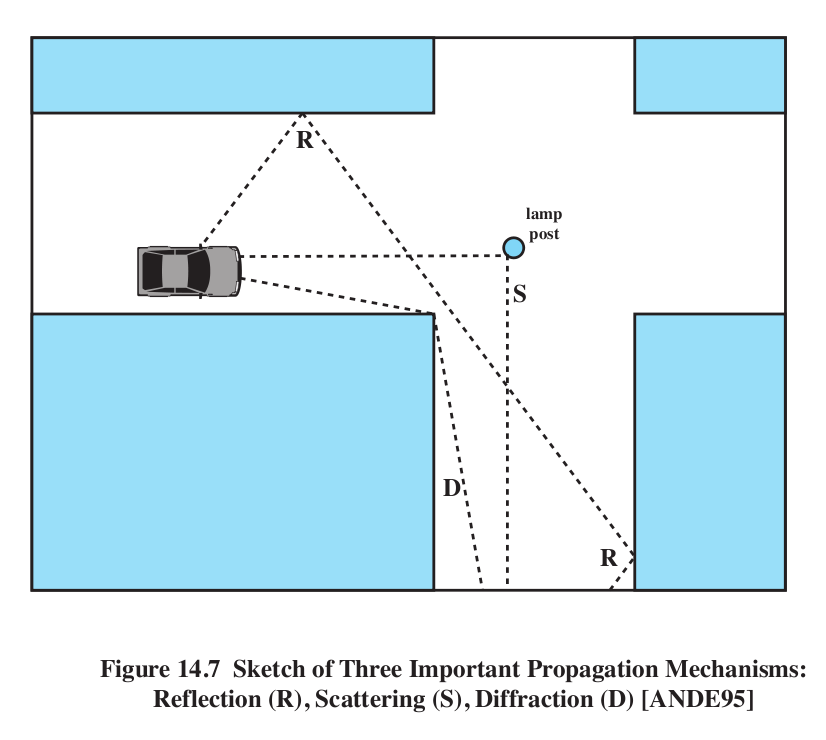
Multipath distortion:
- reflection
- diffraction
- scattering
Stallings Figure 14.7. Note there is no direct path in this figure!
Normally, the reflected path is the worst offender, when compared with the
direct path.
Phase distortion: multipath can lead to different copies arriving sometimes
in phase and sometimes out of phase (this is the basic cause of "fast
fading").
Intersymbol interference (ISI) and Fig 14.8. Pulses might be sent 1 unit
apart, but multipath distortion might create "echo" pulses at times, say,
0.3, 0.5 and 0.9 units following the original pulse. That last echo is
likely to interfere with the next data pulse.
Note that CDMA requires good power control
by the phones so that all signals are roughly equal when received at the
cell tower. Phones all adjust signal strength downwards if received base
signal is stronger than the minimum.
Go through Andrews presentation at http://users.ece.utexas.edu/~jandrews/publications/cdma_talk.pdf
- Walsh codes at base station (below)
- PN codes in receivers (because we no longer can guarantee
synchronization)
- Frequency reuse issues
SMS (text messaging)
This originated as a GSM protocol, but is now universally available under
CDMA as well, and these can be transmitted within SS7. Basically, the
message piggybacks on "system" packets.
Walsh Codes
How are we going to get orthogonal codes? I tried (using brute-force search)
to find a third code orthogonal to the length-6 A&C above or to A&B;
there are none!
If k is a power of 2, we can do this with Walsh
codes. We will create a k×k matrix of +1 and -1 where all the rows
are orthogonal. This is done recursively.
k=1: the matrix is just [+]
k=2: the matrix is
k=4:
+
|
+
|
+
|
+
|
+
|
−
|
+
|
−
|
+
|
+
|
−
|
−
|
+
|
−
|
−
|
+
|
k=2r. Let M be the Walsh matrix of size 2r-1. Arrange
four copies of M in a 2r × 2r matrix as follows, where
−M is the result of flipping every entry in M:
Note that this is what we did to go from k=1 to k=2 above, and from k=2 to
k=4.
GSM phones
GSM uses a fully-packetized approach to transmitting voice. The part that
corresponds to the CDMA mechanisms we looked at last week is known as GPRS:
General Packet Radio Service.
When a call is in progress, the cell-to-tower and tower-to-cell directions
are each assigned a frequency channel. Within that channel, each transmits
packetized voice.
For the tower-to-cell direction (where CDMA uses the complicated
linear-algebra strategy), there are no collisions: the tower is the only
transmitter. The tower can arrange for the sequencing of packets however it
wishes, with the understanding that a tower cannot keep accepting calls
indefinitely as it will run out of bandwidth for transmission.
For the cell-to-tower direction, some mechanism must be in place to limit
packet collisions. This is done using Reservation-ALOHA, derived from
Slotted Aloha. The original ALOHA protocol allowed for an effective
bandwidth utilization of about 1/2e ~ 13.5%. Slotted ALOHA doubled this by
having everyone coordinate transmission attempts so they always started on
slot boundaries.
Reservation-ALOHA entails having mobiles make reservations, which gives them
predictable options to transmit. A mobile device might be allowed to
transmit one in every N slots, for a modestly large N.
CDMA is to power control as GSM is to timing
control
CDMA may use the linear algebra approach from mobile to base if
possible. This may depend on relatively few users moving fast, for
example.
Wi-Fi, Wi-Fi PCF and WiMAX/LTE
In standard "infrastructure" Wi-Fi, stations directly communicate only with
the access point (AP).
Normally Wi-Fi resolves contention with collisions.
Also, two ordinary (non-AP) stations are supposed to at least try to be
aware of each others' presence; this helps reduce collisions.
Wi-Fi
PCF is a Wi-Fi mode of operation in which stations do not transmit
unless "polled" by the AP. If there are no competing Wi-Fi's on the same
channel set, this in principle means collision-free operation.
WiMAX/LTE:
- RTT is too long (Wi-Fi max range: 0.1 Km; WiMAX max range: 10-50 Km)
- uplink scheduling
- ranging
- network entry and collisions
- mobility
- handoffs
- range change
- doppler





