Comp 163 Final Exam Study Guide
Probability
notes by me
Readings from Levin:
Chapter 4: Graph Theory
4.1: Basic facts
4.2: Trees (= graphs with no
cycles)
4.3: Planar graphs
4.4: Graph coloring
4.5: Euler paths/circuits and
Hamiltonian paths
There may also be straightforward questions about
modular arithmetic. There will not be questions from Levin
chapters 1 and 2, though some material about (n choose k) might
show up in a probability question.
Some sample problems
Solutions coming soon.
1. If you deal 8 cards, how many ways can you deal
6 cards of one suit (with the other two cards in the three remaining
suits)?
2. (a) If you roll two dice, how many ways can you
get two 2's?
(b). If you roll two dice, how many ways can you
get a 2 and a 3?
(c). What is the probability of each event above?
3. You have two dice, each of which has the numbers
1, 2 and 3 each appearing twice.
(a). If you roll the two dice, how many outcomes
are there in all?
(b). How many outcomes have at least one 3?
(c). How many outcomes have two 3's?
(d). What is the probability of two 3's, given at
least one 3?
(e). What is the probability of two 3's, without
given any partial information?
4. Among 23 people, the probability of two of them
having the same birthday is just over 50%.
(a). What is the probability on Mars, where the
year has 687 martian days? Work out the probability all the birthdays
are different, below, and subtract from 1. Calculate
(687/687)*(686/687)*...*((687-22)/687)
(b). The year on Saturn has 11,000 saturn days.
Using the birthday-problem approximation, what is the probability that
23 people all have different birthdays?
5. Monty Hall hides a prize behind one of four
doors. Each door is equally likely to be chosen.
(a). What is the probability the prize is behind
door number 1?
(b). You declare that you pick door 1, and Monty
opens doors 2 and 4, revealing nothing. What is the probability the
prize is behind door 1, given this event? What is the probability it is
behind door 3, given this event? (Hint: one of these probabilities is completely
unaffected by the event.)
6. A large hash table that is to contain N items
has size 2N. How many hash buckets are likely to be empty? (Use the
Poisson distribution, with λ=0.5.
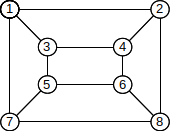
7. Which graphs are bipartite? For those that are,
give a coloring of the vertices using two colors.
(a)
(b)
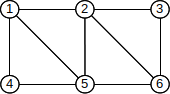
8. For each of the graphs below, find a coloring
with 3 colors. No two nodes connected by an edge can have the same
coloring. To describe your coloring, list the nodes of each color.
(a).
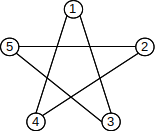
(b).
9. Find an Euler path for the following graph. List
the edges in the order of the path (or the vertices).
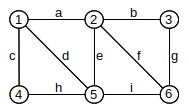
10. Which of the following (multi)graphs have an
Euler path? (You do not have to find it)
(a)
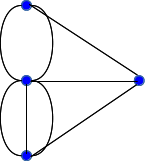
(b)
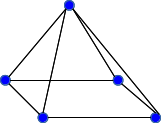
11. A planar graph has 10 vertices and 6 faces.
(a) How many edges must it have?
(b). Assume each face must have a perimeter of at
least 3 edges. Given that each edge appears in exactly 2 face
perimeters, what inequality can you write about the graph?
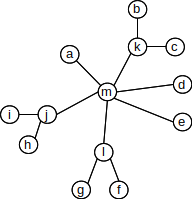
12. The following graph is a tree.
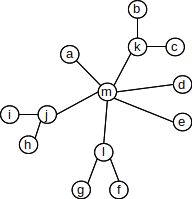
(a). Let k be the designated root vertex, and give
the distance of notes e, f, i, j, l to k.
(b). Now let g be the designated root, and give the
distance to b, k, l, m.
(c). Give a coloring of the graph with two colors.
List what vertices get each color.
13. Give a spanning tree for the following graph.
To express your answer, list the edges you are keeping.
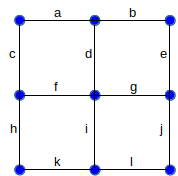
14. Give an example of a graph which has a vertex
of degree 4, and yet which can be drawn with only 2 colors.